RELATIONS AND FUNCTIONS PROBLEMS FOR ALGEBRA 2

Problem 1 :

Given the relation R = {(-2, 3) (a, 4) (1, 9) (0, 7)} which replacement for a makes this relation a function ?

a)  1    b) -2     c)  0      d) 4

Solution :

Applying option a :

Here a = 1

R = {(-2, 3) (1, 4) (1, 9) (0, 7)}

It is not function, because 1 is having two outputs.

Applying option d :

Here a = 4

R = {(-2, 3) (4, 4) (1, 9) (0, 7)}

It is a function, because no input has more than one output.

Problem 2 :

Which relation is not a function ?

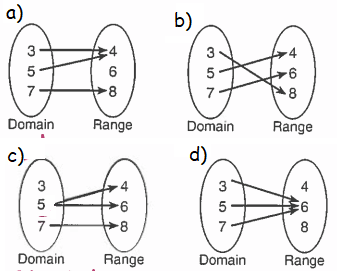
Solution :

By observing the arrow diagrams, option c the input 5 is having two different outputs 4 and 6. So, it is not a function.

Problem 3 :

If f(x) = x² - 2x + 3, find the value of f(-2) 

Solution :

f(x) = x² - 2x + 3

f(-2) = (-2)² - 2(-2) + 3

= 4 + 4 + 3

= 11

So, the value of f(-2) is 11.

Problem 4 :

If f(x) = (x - 2) / (x + 1), then the value of f(n + 1) is equal to 

Solution :

Problem 5 :

If f(x) = 4x² - x + 1, then f(a + 1)  = ?

Solution :

f(x) = 4x² - x + 1

f(a + 1) = 4(a+1)² - (a+1) + 1

= 4(a² + 2a + 1) - (a+1) + 1

= 4a² + 8a + 4 - a - 1 + 1

= 4a² + 7a + 4

Problem 6 :

If f(x) = x² - 3x, find f(x/2)

Solution :

f(x) = x² - 3x

f(x/2) = (x/2)² - 3(x/2)

= x²/4 - 3x/2

Problem 7 :

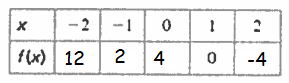
1)  Find the following values of the function.

i) f(2) =    ii)  f(0) = 

2) For which of the values of x is this statement true ?

f(x) = 2

Solution :

1)  i) f(2) = -4   ii)  f(0) = 4

2)  By observing the table, 2 is the output for -1.

f(-1) = 2

Problem 8 :

If the domain of f(x) = 2x + 3 is {-1, 0, 2} which number is not in range ?

a)   1      b)  2     c)  3      d)  7

Solution :

f(x) = 2x + 3

Range = {1, 3, 7}

In this range, 2 is not one of the element. So, option b is correct.

Problem 9 :

The function is defined by the equation y = 8x - 3. If the domain is 2 ≤ x ≤ 4, find the minimum value in the range, find the minimum value in the range of the function.

Solution :

y = 8x - 3

Domain = {2, 3, 4}

The minimum value in the range is 13.

Problem 10 :

Find the inverse of the following function

{(2, 6) (-3, 4) (-7, -5)}

Solution :

Let f(x) = {(2, 6) (-3, 4) (-7, -5)}

Relationship between the function and its inverse :

Domain of f(x) = range of inverse

range of f(x) = domain of inverse

f^-1(x) = {(6, 2) (4, -3) (-5, -7)}

Problem 11 :

Find the inverse of the function

y = 3x + 2

Solution :

Problem 12 :

In which of the following graphs 

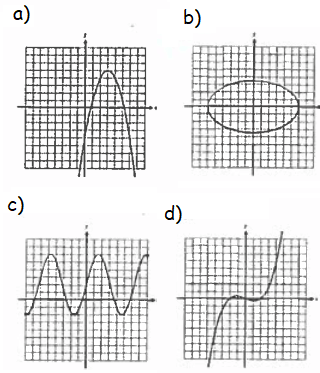
Solution :

Using vertical line test, the vertical should intersect the curve maximum at one point. 

So, option b is not a function..

Problem 13 :

Which graph is not a function.

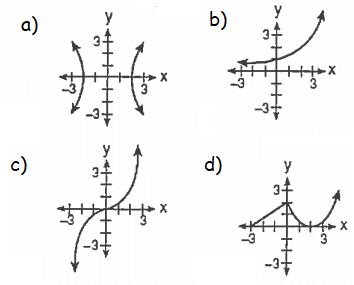
Solution :

Option a is not a function.

Problem 14 :

Which graph represents one to one function 

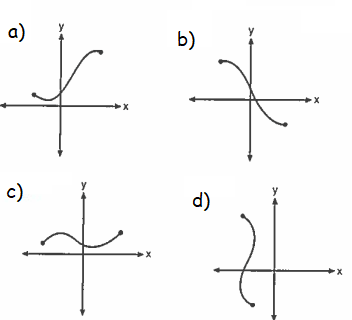
Solution :

Option a :

Using vertical line test, it is function. Using horizontal line test, it is not one to one function.

Option b :

Using vertical line test, it is function. Using horizontal line test, it is one to one function.