PRACTICE PROBLEMS ON SOLVING EXPONENTIAL EQUATIONS

Solve each of the following equation.

Problem 1 :

4^2x+3 = 1

Solution

Problem 2 :

5^3-2x = 5^-x

Solution

Problem 3 :

3^1-2x = 243

Solution

Problem 4 :

3^2a = 3^-a

Solution

Problem 5 :

4^3x-2 = 1

Solution

Problem 6 :

4^2p = 4^-2p-1

Solution

Problem 7 :

6^-2a = 6^2-3a

Solution

Problem 8 :

2^2x+2 = 2^3x

Solution

Problem 9 :

6^3m ⋅ 6^-m = 6^-2m

Solution

Problem 10 :

2^x/2^x = 2^-2x

Solution

Problem 11 :

10^-3x ⋅ 10^x = 1/10

Solution

Problem 12 :

3^-2x+1 ⋅ 3^-2x-3 = 3^-x

Solution

Problem 13 :

Consider the equation 9^m/9ⁿ = 9²

a. Find two numbers m and n that satisfy the equation.

b. Describe the number of solutions that satisfy the equation. Explain your reasoning.

Solution

Problem 14 :

Find the value of x that makes 8^3x/8^{2x + 1} = 8⁹ true. Explain how you four your answer.

Solution

Problem 15 :

Which of the following is equivalent to

7^x ⋅ x⁷ / 7⁷ ⋅ x^x  ?

a)  1      b)  (x - 7)^7/x     c)  (x/7)^{x - 7}   d)  (7/x)^{x - 7}

Solution

Problem 16 :

If 

(3ab²) ⋅ (2a²  b)³  / 8a² b²  = 3a^mbⁿ ?

what is the value of m + n ?

Solution

Problem 1 :

2x^(2/3) = 8

Solution

Problem 2 :

4x^(3/2) = 32

Solution

Problem 3 :

x^1/4 + 3 = 0

Solution

Problem 4 :

2x^3/4 - 14 = 40

Solution

Problem 5 :

(x + 6)^1/2 = x

Solution

Problem 6 :

(5 - x)^1/2 – 2x = 0

Solution

Problem 7 :

2(x + 11)^1/2 = x + 3

Solution

Problem 8 :

(5x² – 4)^1/4 = x

Solution

Problem 9 :

x^1/5 = 2

Solution

Problem 10 :

2√(3x – 1) + 3 = 11

Solution

Problem 11 :

4x² = 64

Solution

Problem 12 :

 2(x – 2)⁴ – 3 = 159

Solution

Problem 13 :

√(2x + 4) = √(x + 2)

Solution

Problem 14 :

 ∛x – 6 = -2

Solution

Solve the following and find extraneous solutions.

Problem 1 :

Solve (2x)^3/4 + 2 = 10

Solution

Problem 2 :

(x + 30)^1/2 = x

Solution

Problem 3 :

(3x)^1/3 = -3

Solution

Problem 4 :

(x + 6)^1/2 = x

Solution

Problem 5 :

(x + 2)^3/4 = 8

Solution

Problem 6 :

(1/5) x^3/4 - 31 = -6

Solution

Problem 7 :

(1/4)^3x = 8^{-2x + 3}

Solution

Problem 8 :

The surface area S (in square centimeters) of a mammal can be modeled by

S = km^2/3

where m is the mass (in grams) of the mammal and k is a constant. The table shows the values of k for different mammals

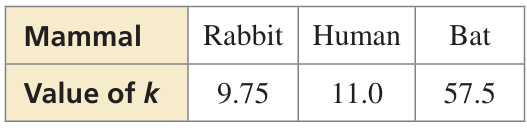
a. Find the surface area of a bat whose mass is 32 grams.

b. Find the surface area of a rabbit whose mass is 3.4 kilograms (3.4 × 10³ grams).

c. Which mammal has the greatest mass per square centimeter of surface area, the bat in part (a), the rabbit in part (b), or a human whose mass is 59 kilograms?

Solution

Problem 1 :

If 3^a+1 = 3^-a+7, what is the value of a ?

Solution

Problem 2 :

If 3^x+2 = y, then what is the value of 3^x in terms of y ?

(a) y+9  (b) y-9  (c) y/3  (d)  y/9

Solution

Problem 3 :

If 2a-b = 4, what is the value of 4^a/2^b

Solution

Problem 4 :

If 2^x+3 - 2^x = k(2^x), what is the value of k ?

Solution

Problem 5 :

If 

√(x√x) = x^a

then what is the value of a ?

Solution

Problem 6 :

If n³ = x and n⁴ = 20x, where n > 0, what is the value of x ?

Solution

Problem 7 :

Solve for x, 2(4^2x+1) = 128

Solution

Problem 8 :

12^2x-1 = (∜12)^x

Solution

Problem 9 :

3^4x+3 = 81^x

Solution

Problem 10 :

12 ⋅ 2^x-7 = 24

Solution

Problem 11 :

If (-a² b³) ⋅ (2a b²) (-3b) = ka^m bⁿ

What is the value of m + n ?

Solution

Problem 12 :

If (2/3 a² b)² ⋅ (4/3 ab)^-3 = ka^m bⁿ

What is the value of k ?

Solution

Problem 13 :

If (x³) (-y)² z^-2 /(x)^-2 y³ z = x^m / yⁿ z^p

What is the value of m + n + p ?

Solution

Problem 14 :

If 3^(a + b)² / 3^(a - b)² = 243, what is the value of ab ?

a)  5/4   b)  3/2     c)  7/4     d)  2

Solution