SOLVING EQUATIONS WITH EXTRANEOUS SOLUTION WITH RATIONAL EXPONENTS

Problem 1 :

Solve (2x)^3/4 + 2 = 10

Solution :

(2x)^3/4 + 2 = 10

(2x)^3/4 = 10 – 2

(2x)^3/4  = 8

Take power 4 on both sides.

((2x)^3/4)⁴ = (8)⁴

 (2x)³ = (8)⁴

(2x)³ = 8 ⋅ 8 ⋅ 8 ⋅ 8

 2x = ∛(8 ⋅ 8 ⋅ 8 ⋅ 8)

 2x = 8∛8

2x = 8∛(2 ⋅ 2 ⋅ 2)

 2x = 8 (2)

2x = 16

x = 16/2

x = 8

When x = 8

 (2x)^3/4 + 2 = 10

(2(8))^3/4 + 2 = 10

(16)^3/4 + 2 = 10

(2⁴)^3/4 = 10 – 2

2³ = 8

8 = 8

There is no extraneous solution.

Problem 2 :

(x + 30)^1/2 = x

Solution:

(x + 30)^1/2 = x

Raise both sides to the power 2.

((x + 30)^1/2)² = (x)²

x + 30 = x²

x² – x – 30 = 0

(x - 6) (x + 5) = 0

x = 6 and x = -5

So, the extraneous solution is -5.

Problem 3 :

(3x)^1/3 = -3

Solution :

(3x)^1/3 = -3

Raise both sides to the power 3.

((3x)^1/3)³ = (-3)³

3x = -27

x = -27/3

x = -9

When x = -9,

(3x)^1/3 = -3

(3(-9))^1/3 = (-27)^1/3 

-3 = -3

So x = -9 is satisfied.

Problem 4 :

(x + 6)^1/2 = x

Solution :

(x + 6)^1/2 = x

Raise both sides to the power 2.

((x + 6)^1/2)² = (x)²

x + 6 = x²

x² – x – 6 = 0

(x + 2) (x – 3) = 0

x = -2 and x = 3

So, 3 is the extraneous solution.

Problem 5 :

(x + 2)^3/4 = 8

Solution :

Given, (x + 2)^3/4 = 8

Raise both sides to the power 4.

((x + 2)^3/4)⁴ = (8)⁴

(x + 2)³ = (8)⁴

(x + 2)³ = 8 ⋅ 8 ⋅ 8 ⋅ 8

x + 2 = ∛(8 ⋅ 8 ⋅ 8 ⋅ 8)

x + 2 = 8∛8

x + 2 = 8∛(2 ⋅ 2 ⋅ 2)

x + 2 = 8 × 2

x + 2 = 16

x = 16 – 2

x = 14

When x = 14,

(x + 2)^3/4 = 8

(14 + 2)^3/4 = 8

(16)^3/4 = 8

(2⁴)^3/4 = 8

(2)³ = 8

8 = 8

So x = 14 satisfied.

Problem 6 :

(1/5) x^3/4 - 31 = -6

Solution :

(1/5) x^3/4 - 31 = -6

(1/5) x^3/4 = -6 + 31

(1/5) x^3/4 = 25

Multiplying by 5, we get

x^3/4 = 25(5)

x^3/4 = 125

(x^1/4)³ = 5³

x^1/4 = 5

Raising power 4 on both sides, we get

x = 5⁴

x = 625

Problem 6 :

(1/4)^3x = 8^{-2x + 3}

Solution :

(1/4)^3x = 8^{-2x + 3}

(1/2²)^3x = (2³)^{-2x + 3}

(2^-2)^3x = (2³)^{-2x + 3}

2^-6x = 2^{-6x + 9}

Equating the exponents, we get

-6x = -6x + 9

-6x + 6x = 9

0x = 9

There is no solution.

Problem 7 :

The surface area S (in square centimeters) of a mammal can be modeled by

S = km^2/3

where m is the mass (in grams) of the mammal and k is a constant. The table shows the values of k for different mammals

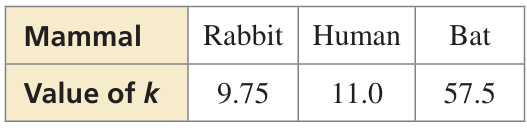
a. Find the surface area of a bat whose mass is 32 grams.

b. Find the surface area of a rabbit whose mass is 3.4 kilograms (3.4 × 10³ grams).

c. Which mammal has the greatest mass per square centimeter of surface area, the bat in part (a), the rabbit in part (b), or a human whose mass is 59 kilograms?

Solution :

S = km^2/3

a) From the table, the value of k for bat = 57.5 and m = 32

S = 57.5(32)^2/3

= 57.5(2⁵)^2/3

= 57.5(2^10/3)

= 57.5(10.05)

= 578.22 grams

1 gram square = 1 cm square

So, the required surface area is 578.22 square cm.

b)  From the table, the value of k for rabbit = 9.75 and m = 3.4 × 10³

m = 3.4 x 1000

= 3400 grams

S = 57.5(32)^2/3

= 57.5(2⁵)^2/3

= 57.5(2^10/3)

= 57.5(10.05)

= 578.22 grams

So, the required surface area by rabbit is 578.22 square cm.

c)  From the table, the value of k for human = 11 and m = 59 kilograms

= 59 x 1000

= 59000 grams

S = 11(59000)^2/3

= 11(1504.4)

= 16549 square cm

Comparing these three human has the greatest mass per square centimeter of surface area.