PRACTICE PROBLEMS ON RATIO AND PROPORTION

Problem 1 :

Bob has 12 red cards and 20 green cards. What is the ratio of Bob's red cards to this green cards ?

Solution

Problem 2 :

In a party 10 soft drinks are required for every 12 guests. If there are 252 guests, how many soft drinks is required.

Solution

Problem 3 :

In Jack's class, 18 of the students are tall and 10 are short. In Michael's class 54 students are tall and 30 students are short. Which class has a higher ratio of tall to short students ?

Solution

Problem 4 :

The price of 3 apples at the Quick Market is $1.44. The price of 5 of the same apples at Walmart is $2.50. Which place is the better buy ?

Problem 5 :

The bakers at the Bakery can make 160 bagels in 4 hours. How many bagels can they bake in 16 hours? What is the rate per hour ?

Solution

Problem 6 :

The ratio of the boys to girls in a class is 2 : 3. If there are 18 boys in the class, how many girls  are in that class ?

Solution

Problem 7 :

The ratio of red marbles to blue marbles in the bag is 3 : 4. If there are 42 marbles in the bag, how many of the marbles are red ?

Solution

Problem 8 :

Methane gas contains carbon atoms and hydrogen atoms in the ratio of 1 : 4. A sample of methane gas contains 92 hydrogen atoms. How many carbon atoms are in the sample? How many total atoms are in the sample?

Solution

Problem 9 :

A nutrition label shows that there are 75 milligrams of sodium in every 12 crackers. You eat 30 crackers. How much sodium do you consume?

Solution

Problem 10 :

Two whole numbers A and B satisfy the following conditions. Find A and B.

A + B = 44

A : B is equivalent to 4 : 7

Solution

Problems on Proportion

Problem 1 :

A car travels 120 miles in 3 hours (with a constant speed). How far will it take to travel 200 miles?

Solution

Problem 2 :

50 apples cost $25. How much would 75 apples cost?

Solution

Problem 3 :

It takes Mike18 minutes to finish reading 4 pages of a book. How long does it take for him to finish reading 30 pages?

Solution

Problem 4 :

Nathan packs 25 boxes in 2 hours. How many boxes can he pack in his 8 – hour shift?

Solution

Problem 5 :

13 candy bars weigh 26 ounces. What is the weight of 35 candy bars?

Solution

Problem 6 :

A machine can produce 6 yards of fabric in 2 minutes. How much fabric can the machine produce in 1 hour?

Solution

Problem 7 :

24 loaves of bread cost $48. How much does 10 loaves cost?

Solution

Problem 8 :

You are making sugar water for your hummingbird feeder. A website indicates to use 4 parts of water for every 1 part of sugar. You use 20 cups of water. How much sugar do you need?

Solution

Problem 1 :

Express as a ratio.

a)  $8 is to $5

b)  7 mL is to 13 mL

c)  5 kg is to 2 kg

Solution

Problem 2 :

a)  65 g is to 1 kg

b)  87 pence is to £1.00

c)  5 months is to 2 years

Solution

Problem 3 :

Write as a ratio.

a)  Peter has $11 and Jacki has $9.

b)  In a theatre, there are 3 girls for every boy.

c)  The school spent €5 on volleyball equipment for every €1 on table tennis equipment.

d)  There are 2 Japanese made cars for every 5 European made cars.

e)  For every 15 km that you travel by car, I can travel 4 km by bicycle.

Solution

Problem 4 :

a)	b)
c)	d)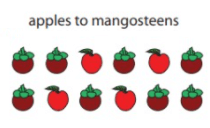
e)

Solution

Problem 5 :

Meg is speedwalking at a pace of 5 meters every 2 seconds. Sean’s pace is 10 meters every 5 seconds. Are they speedwalking at the same pace? If not, who is faster?

Solution

Problem 6 :

You are kayaking at a pace of 63 feet every 12 seconds. Your friend’s pace is 21 feet every 3 seconds. Are you and your friend kayaking at the same pace? If not, who is faster?

Solution

Problem 7 :

Twelve of the 28 students in a class own a dog. What is the ratio of students who own a dog to students who do not? 

Solution

Problem 8 :

Fill in the blank so that the ratios are equivalent.

a)  3 : 9 and 6 : ____

b)  2 : 6 and 8 : ___

c) ___  : 6 and 7 : 2

Solution

Problem 9 :

There are 12 boys and 10 girls in your gym class. If 6 boys joined the class, how many girls would need to join for the ratio of boys to girls to remain the same? Justify your answer

Solution

Problem 10 :

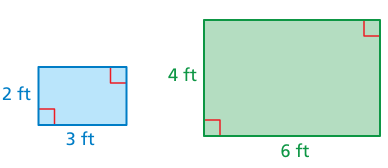
Use the blue and green rectangles.

a. Find the ratio of the length of the blue rectangle to the length of the green rectangle. Repeat this for width, perimeter, and area.

b. Compare your ratios in part (a).

Solution