EXPRESS THE FOLLOWING QUANTITIES AS A RATIO

Problem 1 :

Express as a ratio.

Problem 2 :

a)  65 g is to 1 kg

b)  87 pence is to £1.00

c)  5 months is to 2 years

Solution :

a)

Since the given quantities are different units, first make them the same units.

1 kg = 1000 g

= 65 : 1000

HCF(65, 1000) is 5

= (65/5) : (1000/5)

= 13 :  200

b)

Since the given quantities are different units, first make them the same units.

£1 = 100 pence

= 87 : 100

c)

1 year = 12 months

2 years = 12(2) ==> 24 months

= 5 : 24

Problem 3 :

Write as a ratio.

a)  Peter has $11 and Jacki has $9.

b)  In a theatre, there are 3 girls for every boy.

c)  The school spent €5 on volleyball equipment for every €1 on table tennis equipment.

d)  There are 2 Japanese made cars for every 5 European made cars.

e)  For every 15 km that you travel by car, I can travel 4 km by bicycle.

Solution:

a)  The ratio of Peter and Jacki is 11 : 9

b)  The ratio of girls and boys is 3 : 1

c)  The ratio of volleyball and table tennis is 5 : 1

d)  The ratio of Japanese cars and European cars is 2 : 5

e)  The ratio of distance covered by car to bicycle is 15 : 4

Problem 4 :

	Ratio of books and Pens is 6 : 5
	Ratio of pumpkins and cabbages is 2 :  7
	Ratio of spiders and ladybugs is 5 : 3
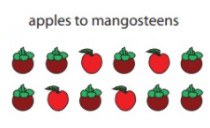	Ratio of apples and mangosteens is 4 : 8 (or) 1 : 2
	Ratio of snow cones and chocolates is 6 : 2 (or) 3 : 1

Problem 5 :

Meg is speedwalking at a pace of 5 meters every 2 seconds. Sean’s pace is 10 meters every 5 seconds. Are they speedwalking at the same pace? If not, who is faster?

Solution:

Distance covered by Meg : Time taken by him

= 5 : 2

Distance covered by Sean : Time taken by him

= 10 : 5

After the simplification, we get

= 2 : 1

So, they are doing the speed walking at the same pace.

= 5 : 2 and 2 : 1

 5/2 = 2/1

Doing cross multiplicaiton,

5 ≠ 4 and (5 > 4)

Then Meg's speed walking is faster at the pace.

Problem 6 :

You are kayaking at a pace of 63 feet every 12 seconds. Your friend’s pace is 21 feet every 3 seconds. Are you and your friend kayaking at the same pace? If not, who is faster?

Solution:

Ratio between distance covered to time :

Kayaking :

63 : 12

= 63/12

= 21/4

Your friend :

= 21 : 3

= 7 : 1

Comparing who is faster :

21/4 = 7/1

Doing cross multiplication, we get

21(7) = 4(1)

147 ≠ 4 (and 147 > 4)

So, Kayaking is faster than your friend.

Problem 7 :

Twelve of the 28 students in a class own a dog. What is the ratio of students who own a dog to students who do not? 

Solution:

Total number of students = 28

Number of students who own dog = 12

Number of students who doesn't own dog = 28 - 12

= 16

Ratio between the number of students who own dog : who dont have 

= 12 : 16

= 3 : 4

Problem 8 :

Fill in the blank so that the ratios are equivalent.

a)  3 : 9 and 6 : ____

b)  2 : 6 and 8 : ___

c) ___  : 6 and 7 : 2

Solution:

a)  3 : 9 and 6 : ____

Let x be the unknown. Since the ratios are equivalent, we can equate the ratios.

3 : 9 = 6 : x

3/9 = 6/x

3x = 6(9)

3x = 54

x = 54/3

x = 18

So, the missing quantity is 18.

b)  2 : 6 and 8 : ___

Let x be the unknwon.

2 : 6 = 8 : x

2/6 = 8/x

2x = 8(6)

2x = 48

x = 48/2

x = 24

So, the missing quantity is 24.

c) ___  : 6 and 7 : 2

Let x be the unknwon 

x : 6 = 7 : 2

x/6 = 7/2

2x = 6(7)

2x = 42

x = 42/2

x = 21

So, the missing quantity is 21.

Problem 9 :

There are 12 boys and 10 girls in your gym class. If 6 boys joined the class, how many girls would need to join for the ratio of boys to girls to remain the same? Justify your answer

Solution:

Number of boys to number fo girls = 12 : 10

After 6 boys joined, let x be the number of girls required to be joined. 

12 + 6 : 10 + x = 12 : 10

18 : (10 + x) = 12 : 10

18/(10 + x) = 12/10

18(10) = 12(10 + x)

180 = 120 + 12x

180 - 120 = 12x

60 = 12x

x = 60/12

x = 5

So, the required number of girls is 5.

Problem 10 :

Use the blue and green rectangles.

a. Find the ratio of the length of the blue rectangle to the length of the green rectangle. Repeat this for width, perimeter, and area.

b. Compare your ratios in part (a).

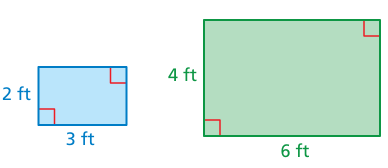
Solution:

Ratio between lenghts of blue to green rectangles :

= 3 : 6

= 1 : 2

Ratio between widths of blue to green rectangles :

= 2 : 4

= 1 : 2

b) Ratio between the perimeter :

= 10 : 20

= 1 : 2

Ratio between the area :

= 6 : 24

= 1 : 4