IDENTIFY THE SHAPES ARE SIMILAR CONGRUENT OR NEITHER WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Tell whether the shapes are similar, congruent or neither.
Problem 1 :
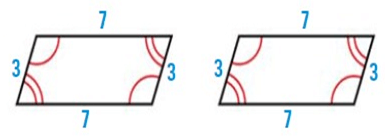
Problem 2 :
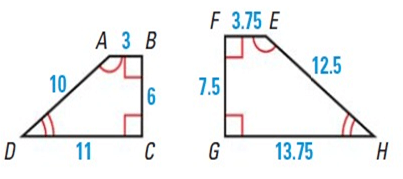
Problem 3 :
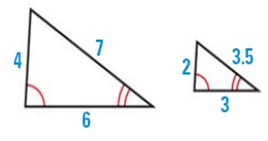
Problem 4 :
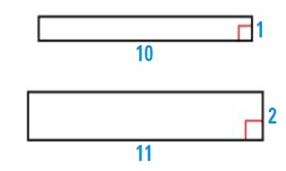
Problem 5 :
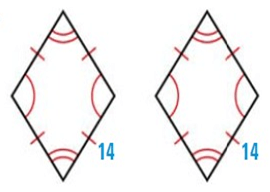
Problem 6 :
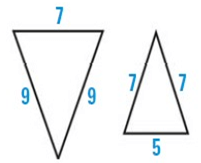
Problem 7 :
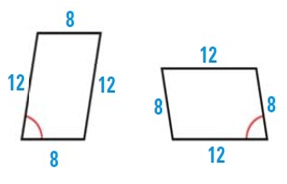
Problem 8 :
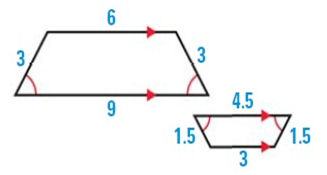
Problem 9 :
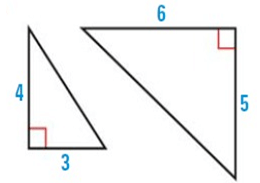
Problem 10 :
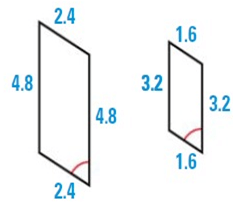
Problem 11 :
In the diagram, ABGH ≅ CDEF.
1. Identify all pairs of congruent corresponding parts.
2. Find the value of x.
3. In the diagram at the left, show that △PTS ≅ △RTQ.
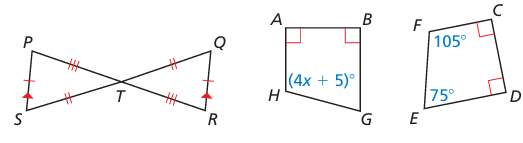
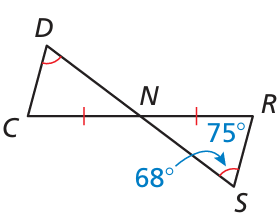
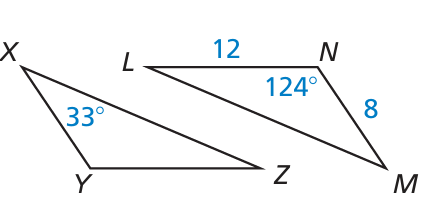
Problem 12 :
a) Find m∠DCN.
b) What additional information is needed to conclude that △NDC ≅ △NSR?
Problem 13 :
△XYZ ≅ △MNL. Copy and complete the statement.
a) m∠M = ______
b) m∠Z = ______
c) XY =
d) m∠Y = ______
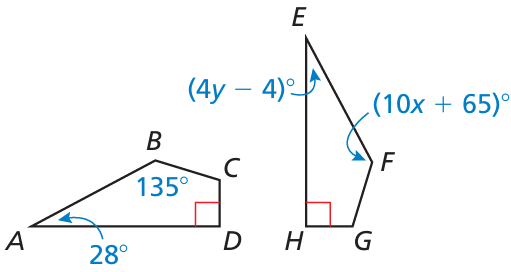
Problem 14 :
Find the values of x and y. ABCD ≅ EFGH
Answer Key
|
1) Congruent 2) Similar 3) Similar 4) neither 5) Congruent |
6) neither 7) Congruent 8) Similar 9) neither 10) Similar |
11)
1) corresponding sides are,
HG and FE
AH and FC
AB and CD
BG and ED
2) x = 25
3)
PT = TR
ST = TQ
PS = QR
Using SSS postulate △PTS ≅ △RTQ.
12) a) 37
b) ND = NS
13)
a) m∠M = 23
b) m∠Z = 23
c) XY = 8
d) m∠Y = 124
14) x = 7 and y = 8
Problem 1 :
Two angles are congruent if they have:
(a) Same name b) Equal measures
(c) Unequal measures (d) None of these
Problem 2 :
If a ∆ ABC ≅ ∆ PQR, then AB is equal to:
(a) QR (b) PQ (c) PR (d) None of these
Problem 3 :
In ∆ ABC and ∆PQR, AB = 4 cm, BC = 5 cm, AC = 6 cm and PQ = 4 cm, QR = 5 cm, PR = 6 cm, then which of the following is true:
(a) ∆ ABC ≅ ∆ QRP (b) ∆ ABC ≅ ∆ PQR
(c) ∆ ABC ≅ ∆ PRQ (d) ∆ ABC ≅ ∆ QPR
Complete the similarity statement for the similar figures and then find the scale factor. Write proportions and solve for missing side lengths.
Problem 4 :
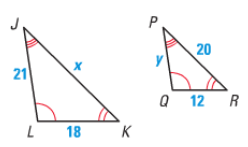
Problem 5 :
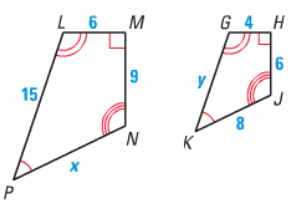
Problem 6 :
Use the given information to write and solve a system of linear equations to find the values of x and y.
a) △LMN ≅ △PQR, m∠L = 40°, m∠M = 90°, m∠P = (17x − y)°, m∠R = (2x + 4y)°
b) △STU ≅ △XYZ, m∠T = 28°, m∠U = (4x + y)°, m∠X = 130°, m∠Y = (8x − 6y)
Problem 7 :
In the diagram, ABEF ≅ CDEF.
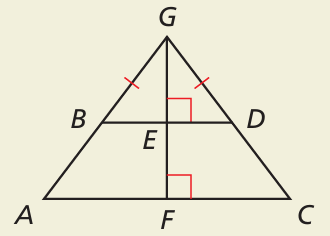
a. Explain how you know that BE ≅ DE and ∠ABE ≅ ∠CDE.
b. Explain how you know that ∠GBE ≅ ∠GDE.
c. Explain how you know that ∠GEB ≅ ∠GED.
d. Do you have enough information to prove that △BEG ≅ △DEG? Explain.
Answer Key
1) Equal measures
2) Corresponding side of AB is PQ.
3) ∆ ABC ≅ ∆ PRQ is correct.
4) x = 30 and y = 14
5) x = 12 and y = 10
6) a) x = 3 and y = 11
b) x = 5 and y = 2
7)
a. Given that ABEF ≅ CDEF,
Since the quadrilaterals are congruent, BE and DE are corresponding parts. Using CPCTC,
BE = DE
∠ABE ≅ ∠CDE
b. In triangles GBE and GDE
GB = GD
∠GEB = ∠GED
BE = DE
So, the triangles GBE and GDE are congruent. Using CPCTC
∠GBE ≅ ∠GDE
c. ∠GEB = ∠GED are right angles
d. Yes, we have enough information to prove △BEG ≅ △DEG
GB = GD
∠GEB = ∠GED
BE = DE
Problem 1 :
Lance and Alien is 5 feet tall. His shadow is 8 feet long.
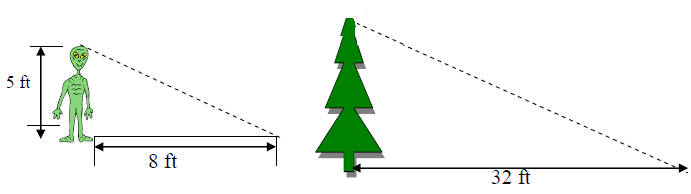
At the same time of day, a tree's shadow is 32 feet long. What is the height of the tree ?
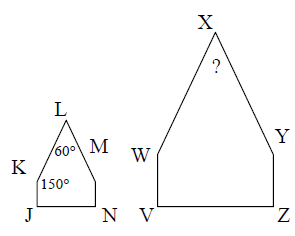
Problem 2 :
Pentagon JKLMN is similar to pentagon VWXYZ, what is the measurement of angle X ?
Problem 3 :
Triangle PQR is similar to triangle DEF as shown.
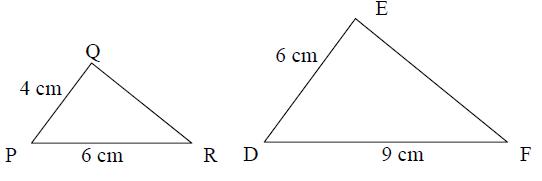
which describes the relationship between the corresponding sides of the two triangles ?
a) PQ/DE = 4/6 b) PQ/DE = 6/4
c) PQ/EF = 4/9 d) PR/DE = 6/6
Problem 4 :
A six foot tall person is standing next to flag pole. The person is casting a shadow 1 1/2 feet in length while a flagpole is casting a shadow 5 feet in length. How tall is the flagpole ?
a) 30 ft b) 25 ft c) 20 ft d) 15 ft
Problem 5 :
The angle of the roof on Kaya's doll house is 56°. She built a scale model of the doll house with a scale ratio of 1 : 4, what is the measure of the angle of the roof of the model ?
a) 14° b) 34° c) 56° d) 224°
Problem 6 :
In triangle PQR is similar to XYZ.
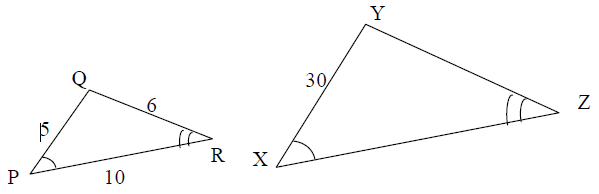
What is the perimeter of XYZ ?
a) 21 cm b) 63 cm c) 105 cm d) 126 cm
Problem 7 :
If the triangles ADE and ABC shown in the figure below are similar, what is the value of x ?
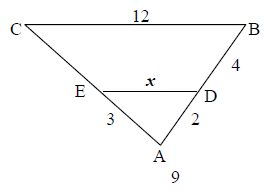
a) 4 b) 5 c) 6 d) 8 e) 10
Problem 8 :
In the figure given below, the two triangles are similar. What is the value of x ?
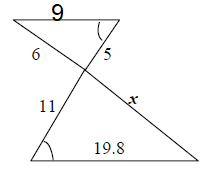
a) 12.4 b) 13.2 c) 14 d) 18.6 e) 22.1
Problem 9 :
Mr. Smith is having some photos enlarged for studio. He wants to enlarge a photo that is 5 inches by 7 inches so the dimensions are 3 times larger than the original. How many times larger than the original photo will the area of the new photo be ?
a) 3 b) 6 c) 9 d) 30
Problem 10 :
During a total eclipse of the Sun, the moon is directly in line with the Sun and blocks the Sun’s rays. The distance DA between Earth and the Sun is 93,000,000 miles, the distance DE between Earth and the moon is 240,000 miles, and the radius AB of the Sun is 432,500 miles. Use the diagram and the given measurements to estimate the radius EC of the moon.
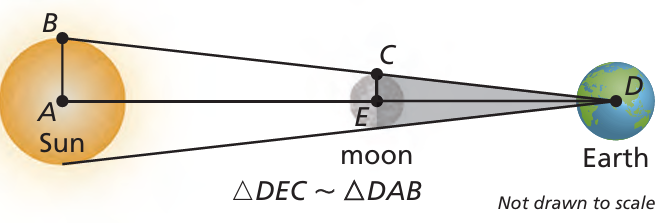
Answer Key
1) h = 20 feet
2) WXY = 60 degree.
3) PQ/DE = 4/6
4) h = 20
5) 56°.
6) perimeter of triangle XYZ = 126 cm.
7) x = 4
8) x = 13.2
9) the new photo is 9 times larger.
10) Approximately the radius of the moon is 1116 miles.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling