DETERMINE IF THE SHAPES SHOWN ARE SIMILAR CONGRUENT OR NEITHER

Tell whether the shapes are similar, congruent or neither.

Problem 1 :

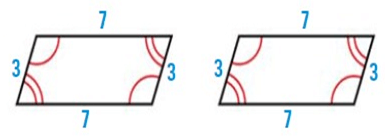
Solution :

As shown, corresponding angles are congruent and corresponding sides are congruent. So, the figures are congruent.

Problem 2 :

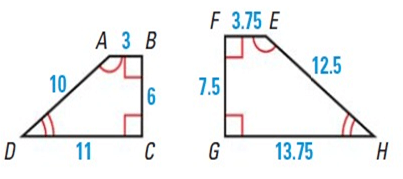
Solution :

As shown, corresponding angles are congruent, but corresponding sides have different lengths. So, the figures are not congruent, but they may be similar.

The figures are similar, if the ratios of the lengths of corresponding sides are equal.

AB/EF = 3/3.75 = 0.8 ----- (1)

BC/FG = 6/7.5 = 0.8 ----- (2)

CD/GH = 11/13.75 = 0.8 ----- (3)

 AD/EH = 10/12.5 = 0.8 ----- (4)

(1) = (2) = (3) = (4)

It has same ratios, so they given shapes are similar.

Problem 3 :

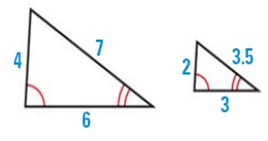
Solution :

As shown, corresponding angles are congruent, but corresponding sides have different lengths. So, the figures are not congruent, but they may be similar.

The figures are similar if the ratios of the lengths of corresponding sides are equal.

4/2 = 2 ----- (1)

7/3.5 = 2 ----- (2)

 6/3 = 2 ----- (3)

(1) = (2) = (3), so the shapes are similar.

Problem 4 :

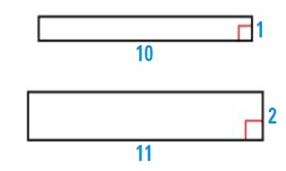
Solution :

As shown, corresponding angles are congruent and corresponding sides are not congruent. So, the figures are neither.

10/11 = 0.91 ----- (1)

1/2 = 0.5 ----- (2)

So, (1), (2) are neither.

Problem 5 :

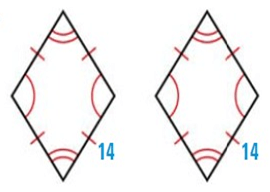
Solution :

As shown, corresponding angles are congruent and corresponding sides are congruent. So, the figures are congruent.

Problem 6 :

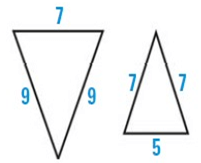
Solution :

As shown, corresponding angles are congruent and corresponding sides are not congruent. So, the figures are neither.

7/5 = 1.4 ----- (1)

9/7 = 1.3 ----- (2)

9/7 = 1.3 ----- (3)

So, (1), (2), (3) are neither.

Problem 7 :

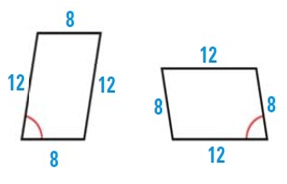
Solution :

As shown, corresponding angles are congruent and corresponding sides are congruent. So, the figures are congruent.

Problem 8 :

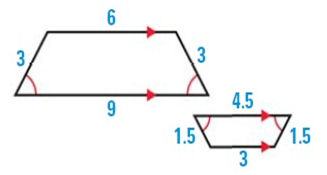
Solution :

As shown, corresponding angles are congruent, but corresponding sides have different lengths. So, the figures are not congruent, but they may be similar.

The figures are similar if the ratios of the lengths of corresponding sides are equal.

6/3 = 2 ----- (1)

3/1.5 = 2----- (2)

3/1.5 = 2 ----- (3)

9/4.5 = 2 ----- (4)

(1) = (2) = (3) = (4), so the shapes are similar.

Problem 9 :

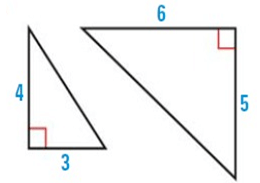
Solution :

As shown, corresponding angles are congruent and corresponding sides are not congruent. So, the figures are neither.

4/5 = 0.8 ----- (1)

6/3 = 2 ----- (2)

So, (1), (2) are neither.

Problem 10 :

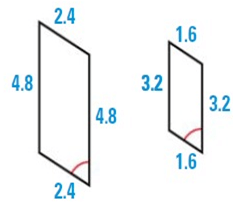
Solution :

As shown, corresponding angles are congruent, but corresponding sides have different lengths. So, the figures are not congruent, but they may be similar.

The figures are similar if the ratios of the lengths of corresponding sides are equal.

2.4/1.6 = 1.5 ------ (1)

4.8/3.2 = 1.5 ----- (2)

4.8/3.2 = 1.5 ----- (3)

2.4/1.6 = 1.5 ----- (4)

(1) = (2) = (3) = (4), so the shapes are similar.

Problem 11 :

In the diagram, ABGH ≅ CDEF.

1. Identify all pairs of congruent corresponding parts.

2. Find the value of x.

3. In the diagram at the left, show that △PTS ≅ △RTQ.

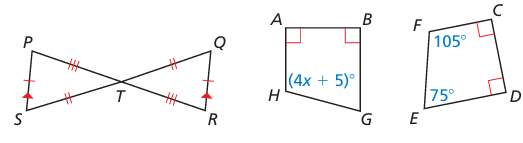
Solution :

In quadrilateral ABGH and FCDE

1) 

corresponding sides are,

HG and FE

AH and FC

AB and CD

BG and ED

2) Obtuse angles are equal,

4x + 5 = 105

4x = 105 - 5

4x = 100

x = 100/4

x = 25

3) Congruent sides are,

PT = TR

ST = TQ

PS = QR

Using SSS postulate △PTS ≅ △RTQ.

Problem 12 :

a) Find m∠DCN.

b) What additional information is needed to conclude that △NDC ≅ △NSR?

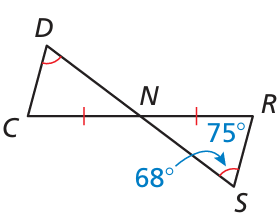
Solution :

a) In triangle NRS,

75 + 68 + ∠RNS = 180

143 + ∠RNS = 180

∠RNS = 180 - 143

= 37

b) ∠DNC = 37 (vertical angles)

NC = NR

We need the information, ND = NS

Problem 13 :

△XYZ ≅ △MNL. Copy and complete the statement.

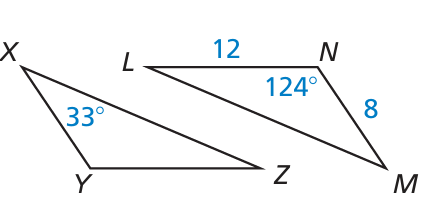
a) m∠M = ______

b) m∠Z = ______

c) XY =

d) m∠Y = ______

Solution :

Since the triangles are congruent,

m∠N = 124 (Obtuse angle),  m∠Y =  m∠N

In triangle XYZ,

∠X + ∠Y + ∠Z = 180

33 + 124 + ∠Z = 180

157 + ∠Z = 180

∠Z = 180 - 157

∠Z = 23 = ∠M

XY = NM = 8

a) m∠M = 23

b) m∠Z = 23

c) XY = 8

d) m∠Y = 124

Problem 14 :

Find the values of x and y. ABCD ≅ EFGH

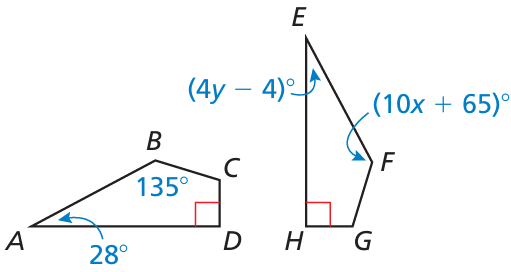
Solution :