FROM THE GIVEN VERTEX AND FOCUS FIND EQUATION OF ELLIPSE WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Find the standard form of the equation of the ellipse with the given characteristics and center at the origin.
Problem 1 :
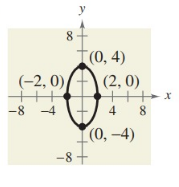
Problem 2 :
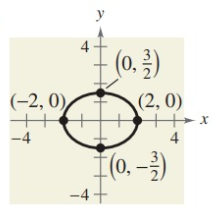
Problem 3 :
Vertices: (±6, 0); foci: (±2, 0)
Problem 4 :
Vertices: (0, ±8); foci: (0, ±4)
Find the standard form of the equation of the ellipse with the given characteristics.
Problem 5 :
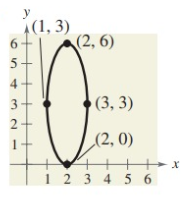
Problem 6 :
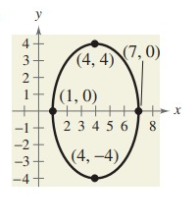
Problem 7 :
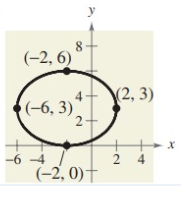
Problem 8 :
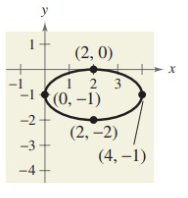
Answer Key
1) x2/4 + y2/16 = 1
2) x2/4 + y2/16 = 1
3) x2/36 + y2/32 = 1
4) x2/48 + y2/64 = 1
5) (x - 2)2/1 + (y - 3)2/9 = 1
6) (x - 4)2/9 + y2/16 = 1
7) (x + 2)2/16 + (y - 3)2/9 = 1
8) (x - 2)2/4 + (y + 1)2/1 = 1
Find the standard form of the equation of each ellipse.
Problem 1 :
Foci (0, ±3), vertices (0, ±5)
Problem 2 :
Major axis horizontal with length 12,length of minor axis 4; center: (-1, 3)
Problem 3 :
Foci (±5, 0), length of major axis 12
Problem 4 :
Endpoints of major axis: (2, 2) & (8, 2), Endpoints of minor axis: (5, 3) & (5, 1)
Problem 5 :
Problem 6 :
Answer Key
1) equation of the ellipse is
2)
3)
4)
5)
6)
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling