FROM THE GIVEN VERTEX AND FOCUS FIND EQUATION OF ELLIPSE

Find the standard form of the equation of the ellipse with the given characteristics and center at the origin.

Problem 1 :

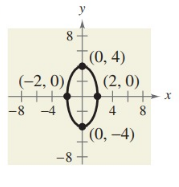
Solution:

Major axis = (0, ±4), Minor axis = (±2, 0)

Major axis a = 4

Minor axis b = 2

The ellipse symmetric about y- axis.

Problem 2 :

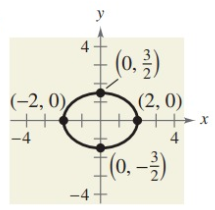
Solution:

Major axis = (±2, 0), Minor axis = (0, ±3/2)

Major axis a = 2

Minor axis b = 3/2

The ellipse symmetric about x- axis.

Problem 3 :

Vertices: (±6, 0); foci: (±2, 0)

Solution:

Given, 

Vertices: (±6, 0)

The vertices are of the form (±a, 0)

a = 6

Hence, the major axis along x-axis.

foci = (±c, 0)

= (±2, 0)

c = 2

b² = a² - c²

b² = 6² - 2²

b² = 36 - 4

b² = 32

Equation of ellipse is

Problem 4 :

Vertices: (0, ±8); foci: (0, ±4)

Solution:

Given, 

Vertices: (0, ±8)

The vertices are of the form (0, ±a)

a = 8

Hence, the major axis along y-axis.

foci = (0, ±c)

= (0, ±4)

c = 4

b² = a² - c²

b² = 8² - 4²

b² = 64 - 16

b² = 48

Equation of ellipse is

Find the standard form of the equation of the ellipse with the given characteristics.

Problem 5 :

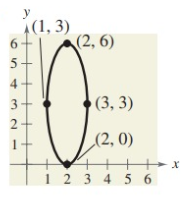
Solution:

Standard equation of ellipse with the center not an origin.

The ellipse symmetric about y- axis.

center (h, k) = (2, 3)

Distance from center to vertex (a) = 3

Distance from center to co-vertex (b) = 1

Problem 6 :

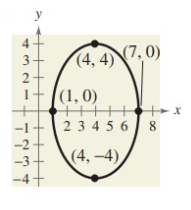
Solution:

Standard equation of ellipse with the center not an origin.

The ellipse symmetric about y- axis.

center (h, k) = (4, 0)

Distance from center to vertex (a) = 4

Distance from center to co-vertex (b) = 3

Problem 7 :

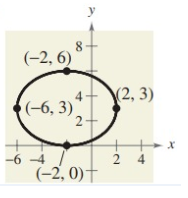
Solution:

Standard equation of ellipse with the center not an origin.

The ellipse symmetric about x- axis.

center (h, k) = (-2, 3)

Distance from center to vertex (a) = 4

Distance from center to co-vertex (b) = 3

Problem 8 :

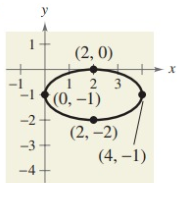
Solution:

Standard equation of ellipse with the center not an origin.

The ellipse symmetric about x- axis.

center (h, k) = (2, -1)

Distance from center to vertex (a) = 2

Distance from center to co-vertex (b) = 1