FINDING TOTAL SURFACE AREA OF A RECTANGULAR PRISM WORKSHEET

Problem 1 :

Solution

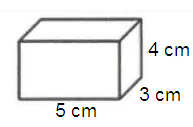
Problem 2 :

Solution

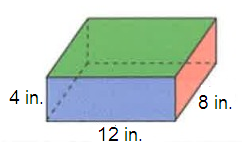
Problem 3 :

Solution

Problem 4 :

Solution

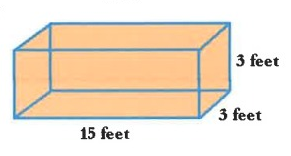
Problem 5 :

Solution

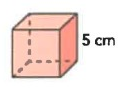
Problem 6 :

Find the surface area of a rectangular prism that has a length of 8 inches, a width of 3 inches, and a height of 6 inches.

Solution

Problem 7 :

A box that is 15 inches wide, 25 inches high, and 2 inches thick is to be wrapped in gift paper. How many square inches of gift paper are needed?

Solution

Problem 8  :

Find the indicated area for the rectangular prism.

a)  Area of Face A

b)  Area of Face B

c)  Area of Face C

d) Surface area of the prism

Solution

Problem 9  :

What is the least amount of wrapping paper needed to wrap a gift box that measures 8 inches by 8 inches by 10 inches? Explain.

Solution

Problem 10  :

A public library has an aquarium in the shape of a rectangular prism. The base is 6 feet by 2.5 feet. The height is 4 feet. How many square feet of glass were used to build the aquarium? (The top of the aquarium is open.)

Solution

Problem 11  :

The material used to make a storage box costs $1.25 per square foot. The boxes have the same volume. How much does a company save by choosing to make 50 of Box 2 instead of 50 of Box 1?

Solution

Problem 1:

The lateral surface area of a cuboid whose length, width  and height are 2a, 2b and 2c respectively is

a)  2(ab + bc + ca)    b)  4(ab + bc + ca)

c)  8(a + b) c     d)  none of these

Solution

Problem 2 :

The sum of the areas of all faces (excluding top and bottom) of a cuboid is the ___________ of the cuboid.

a) Volume      b) lateral surface area

c) Total surface area     d) none of these

Solution

Problem 3 :

The volume of a cuboid whose length, breadth and height are 2a, 3a and 4a is

a)  24a²    b)  24a³     c) 12a³     d) none of these

Solution

Problem 4 :

Find the height of a cuboid whose volume is 756 cm³ and base area is 63 cm²?

Solution

Problem 5 :

The dimension of a cuboid are in the ratio of 2:3:4 and its total surface area is 280 m². Find the dimensions.

Solution

Problem 6 :

A cuboid is 40 cm × 20 cm × 10 cm. what would be the side of a cube having the same volume?

a) 20 cm     b) 40 cm    c) 10 cm    d) 30 cm

Solution

Problem 7 :

A cuboid has a volume of 3000 cm³, with height 15 cm and length 20 cm. Find the area of the upper surface.

Solution

Problem 8 :

The sum of length, breadth and depth of a cuboid is 19 cm and the diagonal is 5√5. Find its surface area.

Solution

Problem 9 :

Three cubes with sides in the ratio 3:4:5 are melted to form a single cube whose diagonal is 12√3 cm. find the sides of the cube.

Solution

Problem 10 :

A company is designing a juice box. The box is in the shape of a rectangular prism. The base of the box is 6 1/2 inches by 2 1/2 inches, and the box is 4 inches high. If juice fills 90% of the box’s volume, find the volume of juice in the box.

Find the 

(i) Lateral surface area and 

(ii)  Total surface area of the following rectangular prism.

Problem 1 :

Solution

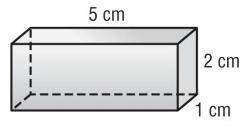
Problem 2 :

Solution

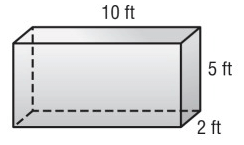
Problem 3 :

Solution

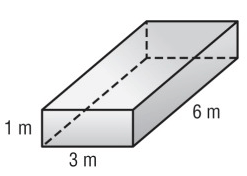
Problem 4 :

Solution

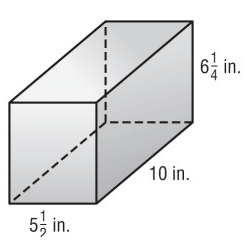
Problem 5 : 

Solution

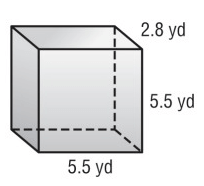
Problem 6 : 

A rectangular room is 12 feet by 21 feet. The walls are 8 feet tall. Paint is sold in one gallon containers. If a gallon of paint covers 450 sqaure feet, how many gallons of paint should poloma buy to paint the walls of the room ?

Solution

Problem 7 : 

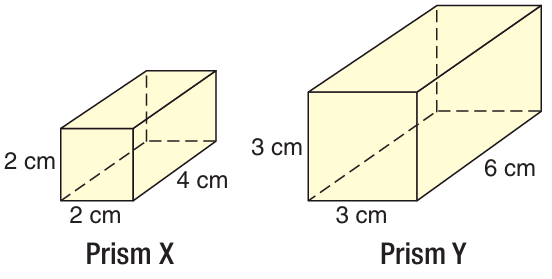
The scale factor of prism X to prism Y is 2/3. What is the ratio of the surface area of prism X to the surface area of prism Y.

Solution

Problem 8 : 

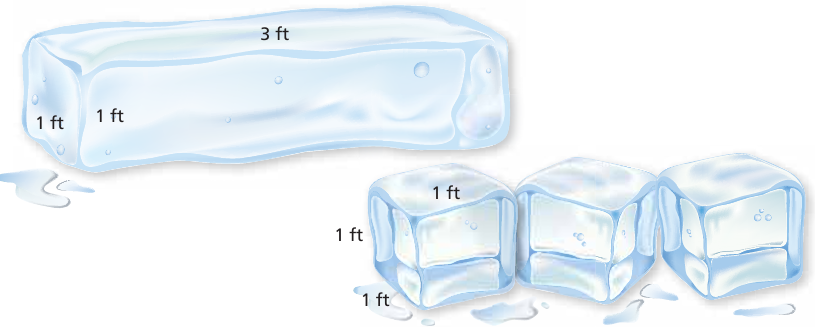
The greater the surface area of an ice block, the faster it will melt. Which will melt faster, the bigger block or the three smaller blocks? Explain your reasoning.

Solution