FINDING AREA OF A REGULAR POLYGON USING SPECIAL RIGHT TRIANGLES

What is polygon ?

A polygon can be defined as a flat or plane, two-dimensional closed shape with straight sides. It does not have curved sides.

Regular polygon :

A polygon having equal sides and equal angles is a regular polygon.

To find area of regular polygon, we use the formula 

What is Apothem ?

A line from the center of a regular polygon at right angles to any of its sides.

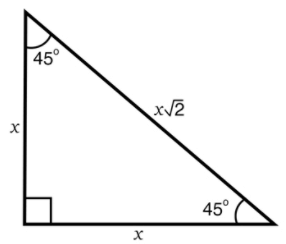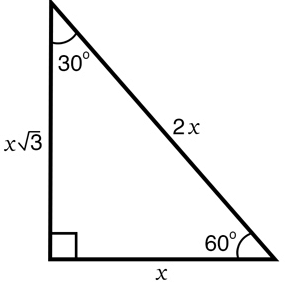To know more about special right triangles, please visit

Special right triangles

Use what you know about special right triangles to find the area of each regular polygon. Leave your answer in simplest form.

Example 1 :

Solution :

Since the given triangle is a regular polygon, every sides will have the same measure. So, it must be a equilateral triangle.

Number of small triangles created by joining 

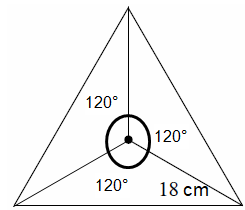
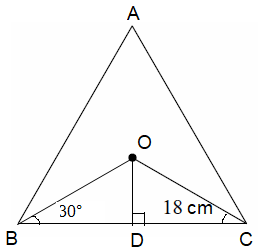
In triangle ODC,

∠ODC = 90, ∠DCO = 30, ∠COD = 60

Smallest side = OD

In 30-60-90 special right triangle, the side which is opposite to 60 is √3(Smaller side).

hypotenuse (OC) = 2(Smallest side)

OC = 2OD

Then,

18 = 2OD and OD = 9

Problem 2 :

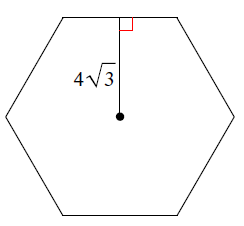
Solution :

Number of sides of a polygon = 6

by drawing lines from center to each vertex, we may draw six triangles of equal measure.

Angle measure of each triangle = 360/6 ==> 60

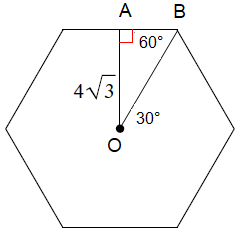
In triangle OAB,

OB = Hypotenuse, smaller side = AB

OB = 2(AB)

In special right triangle, the side which is opposite to 60 is √3(Smaller side).

OA = 4√3 then AB = 4 and OB = 2(4) ==> 8

Side length = 2(4) ==> 8

Problem 3 :

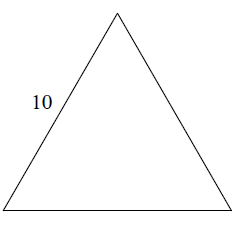
Solution :

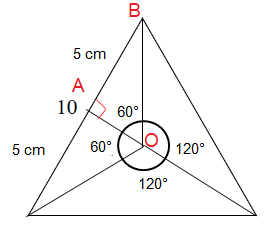
OA is perpendicular bisector, AB = 5 cm

∠AOB = 60, ∠ABO = 30

OA = Smaller side

AB = √3 (Smaller side)

5 = √3 (OA)

OA = 5/√3 (Apothem)

Side length = 10 cm

Problem 4 :

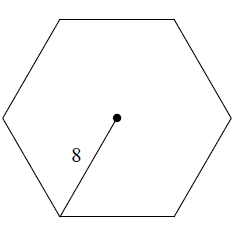
Solution :

Central angle of one triangle = 360/60

= 60 degree

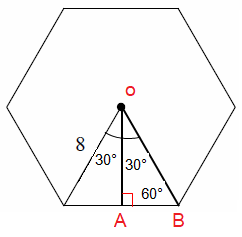
OB = 8, AB = Smaller side

2AB = OB, then AB = 4

OA = 4√3 (Apothem)

Side length = 8

Perimeter = 6(8) ==> 48

Area = (1/2) x 48 x 4√3

= 24 x 4√3

= 96√3 square units.