SPECIAL RIGHT TRIANGLES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
There are two types of special right triangles
- 30 - 60 - 90 right triangle
- 45 - 45 - 90 right triangle
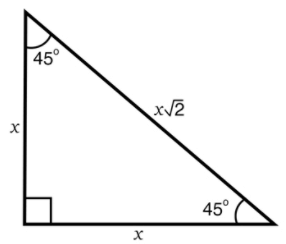
In a 45-45-90 triangle
the hypotenuse is 2 times as long as a leg
An isosceles right triangle is also called a 45-45-90 triangle.
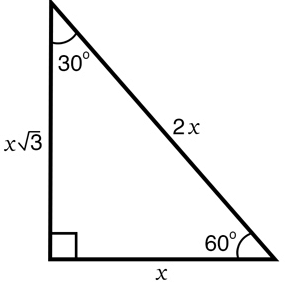
In a 30 - 60 - 90 triangle,
the hypotenuse = twice as long as the shorter leg
and
the longer leg = √3 times as long as the shorter leg.
Find the value of x in each triangle
Problem 1 :
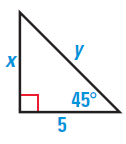
Solution :
It comes under 45-45-90 right triangle.
Hypotenuse (y) = 2(Smallest sides)
y = 2(5)
y = 10
x = 5
Problem 2 :
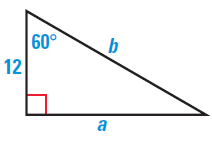
Solution :
It comes under 30-60-90 right triangle.
Hypotenuse = b
Smallest leg = 12
Longer leg (a) = √3(shorter leg)
= 12√3
Hypotenuse = 2(shorter leg)
= 2(12)
= 24
Problem 3 :
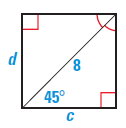
Solution :
Hypotenuse = 8
Shorter leg = c
c = d
Hypotenuse = 2(Shorter leg)
8 = 2c
c = 4 and d = 4
Problem 4 :
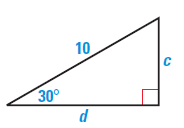
Solution :
Shorter leg = c, hypotenuse = 10, longer leg = d
|
2(Shorter leg) = 10 2c = 10 c = 5 |
Longer leg = √3(5) d = 5√3 |
Problem 5 :
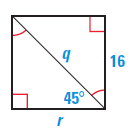
Solution :
Shorter leg = r = 16, hypotenuse = q
Hypotenuse = 2(Shorter leg)
q = 2(16)
q = 32
Problem 6 :
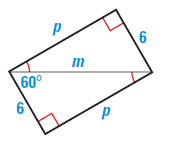
Solution :
Hypotenuse = m
Shorter leg = 6 and
longer leg = p
Hypotenuse = 2(Shorter leg)
m = 2(6)
m = 12
Longer leg = √3 (shorter leg)
P = 6√3
Problem 7 :
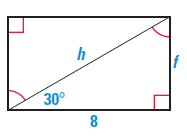
Solution :
Hypotenuse = h
Shorter leg = f and
longer leg = 8
Longer leg = √3 (shorter leg)
8 = √3(f)
f = 8/√3
f = (8/√3) ⋅ (√3/√3)
f = 8√3/3
Hypotenuse (h) = 2(shorter leg)
= 2(8√3/3)
= 16√3/3
Problem 8 :
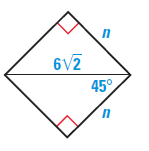
Solution :
Hypotenuse = 6√2
Shorter leg = n
Hypotenuse = 2(Shorter leg)
6√2 = 2n
n = 3√2
Problem 9 :
The side length of an equilateral triangle is 5 cm. Find the length of an altitude of the triangle.
Solution :
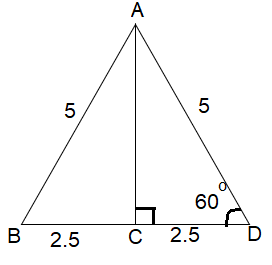
Shorter leg = CD = 2.5
Longer leg = AC
Hypotenuse = AD = 5
Longer leg = √3(Shorter leg)
= √3(2.5)
= 2.5√3
Problem 10 :
The perimeter of the square is 36 inches. Find the length of the diagonal.
Solution :
Let x be the side length of square.
Perimeter of the square = 36
4x = 36
x = 9
Using Pythagorean theorem :
x2 + x2 = (Length of diagonal)2
92 + 92 = (Length of diagonal)2
81 + 81 = (Length of diagonal)2
Length of diagonal = √162
= 9√2
Problem 11 :
The road sign is shaped like an equilateral triangle. Estimate the area of the sign by finding the area of the equilateral triangle.

Solution :
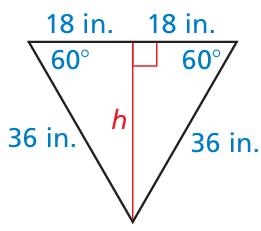
First fi nd the height h of the triangle by dividing it into two 30°- 60°- 90° triangles. The length of the longer leg of one of these triangles is h. The length of the shorter leg is 18 inches.
h = 18 ⋅ √3
= 18 √3
Area = 1/2 bh
= 1/2 (36) (18√3)
≈ 561.18
The area of the sign is about 561 square inches.
Problem 12 :
A tipping platform is a ramp used to unload trucks. How high is the end of an 80-foot ramp when the tipping angle is 30°? 45°?

When the tipping angle is 30°, the height h of the ramp is the length of the shorter leg of a 30°- 60°- 90° triangle. The length of the hypotenuse is 80 feet.
80 = 2h
40 = h
When the tipping angle is 45°, the height h of the ramp is the length of a leg of a 45°- 45°- 90° triangle. The length of the hypotenuse is 80 feet.
80 = h ⋅ √2
80/√2 = h
56.6 ≈ 56 feet 7 inches
When the tipping angle is 30°, the ramp height is 40 feet. When the tipping angle is 45°, the ramp height is about 56 feet 7 inches.
Problem 13 :
The body of a dump truck is raised to empty a load of sand. How high is the 14-foot-long body from the frame when it is tipped upward by a 60° angle?
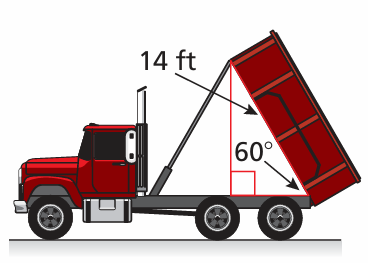
Solution :
In the 30-60-90 right triangle above,
The side which is opposite to 60 degree is √3 (smaller side)
Let half of the base = x (smaller side)
2x = 14
x = 7
Height = √3 (7)
= 7√3
= 7(1.732)
= 12.124 foot
So, the required height is 12.124 foot.
Problem 14 :
A nut is shaped like a regular hexagon with side lengths of 1 centimeter. Find the value of x. (Hint: A regular hexagon can be divided into six congruent triangles.)
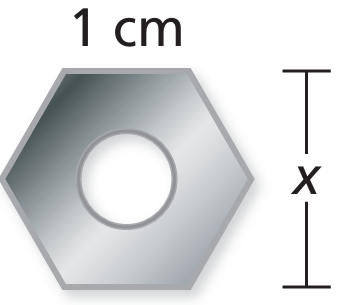
In a hexagon, we have six identitcal triangles. So, each angle measure at the center will be 360/6, that is 60.
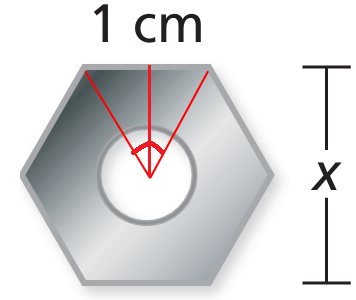
Half of the triangle is 30-60-90 right triangle. Half of the base = 0.5 and half of the height is x/2.
Smaller side = 0.5, side which is opposite to 60 degree = x/2
x/2 = √3(smaller side)
x/2 = √3(0.5)
x = 2√3(0.5)
x = √3
x = 1.732 cm
So, the value of x is 1.732 cm.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling