FINDING SLOPE FROM THE GRAPH

Find the slope of each line.

Problem 1 :

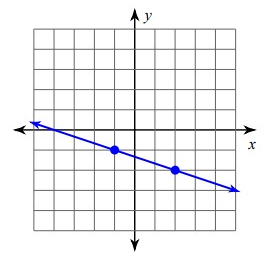
Solution :

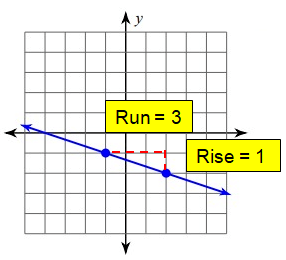
Since it is falling line, it will have negative slope.

Slope (m) = Rise/Run

= -1/3

Problem 2 :

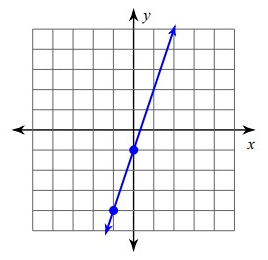
Solution :

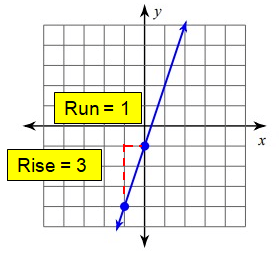
Since it is raising line, it will have positive slope.

Slope (m) = Rise/Run

= 3/1

Problem 3 :

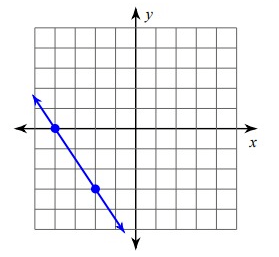
Solution :

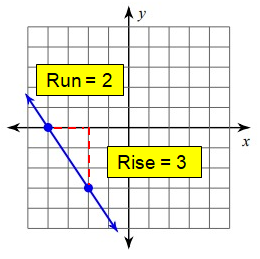
Since it is falling line, it will have negative slope.

Slope (m) = Rise/Run

= -3/2

Problem 4 :

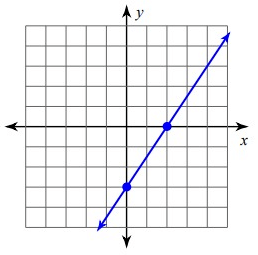
Solution :

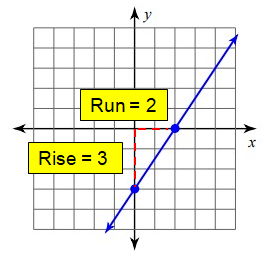
Since it is raising line, it will have positive slope.

Slope (m) = Rise/Run

= 3/2

Problem 5 :

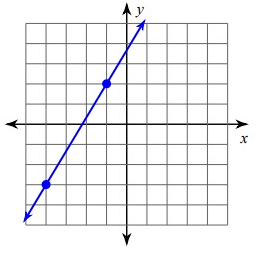
Solution :

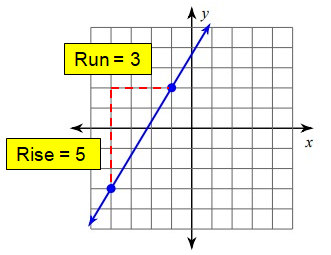
Since it is raising line, it will have positive slope.

Slope (m) = Rise/Run

= 5/3

Problem 6 :

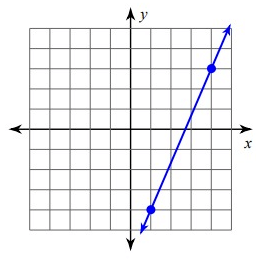
Solution :

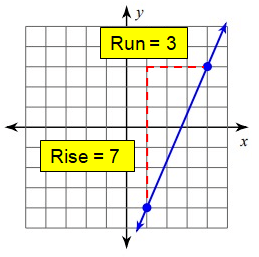
Since it is raising line, it will have positive slope.

Slope (m) = Rise/Run

= 7/3

Describe the slope of the line. Then find the slope.

Problem 7 :

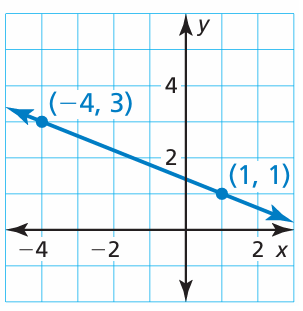
Solution :

By observing the line from left to right, it is a falling line. So, it must have negative slope.

Slope = (y₂ - y₁) / (x₂ - x₁)

Teh two points on the line are (-4, 3) and (1, 1)

= (1 - 3) / (1 - (-4))

= -2 / (1 + 4)

= -2/5

Since we have falling line, we get the slope with negative sign.

Problem 8 :

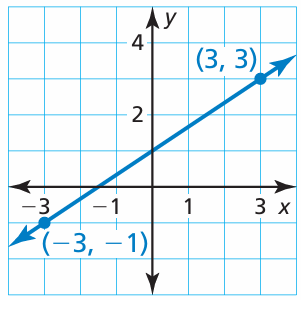
Solution :

By observing the line from left to right, it is a raising line. So, it must have positive slope.

Slope = (y₂ - y₁) / (x₂ - x₁)

The two points on the line are (-3, -1) and (3, 3)

= (3 - (-1)) / (3 - (-3))

= (3 + 1) / (3 + 3)

= 4/6

= 2/3

Since we have raising line, we get the slope with negative sign.

Problem 9 :

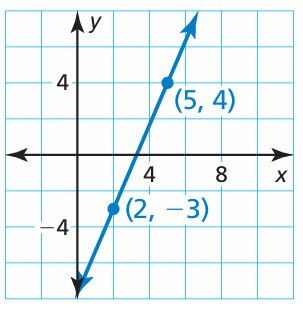
Solution :

By observing the line from left to right, it is a raising line. So, it must have positive slope.

Slope = (y₂ - y₁) / (x₂ - x₁)

The two points on the line are (2, -3) and (5, 4)

= (4 - (-3)) / (5 - 2)

= (4 + 3) / 3

= 7/3

So, the required slope is 7/3.

Problem 10 :

You are ordering shirts for the math club at your school. Short-sleeved shirts cost $10 each. Long-sleeved shirts cost $12 each. You have a budget of $300 for the shirts. The equation 10x + 12y = 300 models the total cost, where x is the number of short-sleeved shirts and y is the number of long-sleeved shirts.

a. Graph the equation. Interpret the intercepts.

b. Twelve students decide they want short-sleeved shirts. How many long-sleeved shirts can you order?

Solution :

10x + 12y = 300

Finding x and y intercepts :

a)

• there must be maximum number of short sleeved shirts be 30
• There must be maximum number of long sleeved shirts be 25.

b)  10x + 12y = 300

When x = 12

10(12) + 12y = 300

120 + 12y = 300

12y = 300 - 120

12y = 180

y = 180/12

y = 15

Problem 11 :

The graph shows the number of miles a helicopter is from its destination after x hours on its first flight. On its second flight, the helicopter travels 50 miles farther and increases its speed by 25 miles per hour. The function

f(x) = 350 − 125x

represents the second flight, where f(x) is the number of miles the helicopter is from its destination after x hours. Which flight takes less time? Explain.

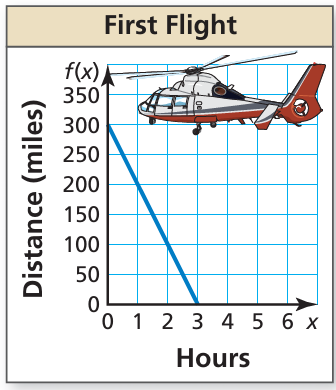
Solution :

You are given a graph of the fi rst fl ight and an equation of the second fl ight. You are asked to compare the fl ight times to determine which flight takes less time.

Graph the function that represents the second fl ight. Compare the graph to the graph of the first flight. The x-value that corresponds to f(x) = 0 represents the fl ight time.

Graph f(x) = 350 − 125x.

Make an input-output table to fi nd the ordered pairs.

Plot the ordered pairs (0, 350) (1, 225) and (2, 100).

Draw a line through the points. Note that the function only makes sense when x and f(x) are positive. So, only draw the line in the first quadrant.

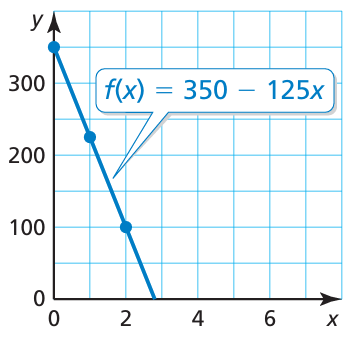
From the graph of the first flight, you can see that when f(x) = 0, x = 3. From the graph of the second fl ight, you can see that when f(x) = 0, x is slightly less than 3. So, the second flight takes less time. 4. Look Back You can check that your answer is correct by fi nding the value of x for which f(x) = 0.

f(x) = 350 − 125x

0 = 350 − 125x

−350 = −125x

x = 2.8

So, the second flight takes 2.8 hours, which is less than 3.