COMPARING LINEAR FUNCTIONS AND GRAPHS

Use that information given to help you compare the two functions and answer the questions about them.

Problem 1 :

Alan and Margot each drive from City A to City B, a distance of 𝟏𝟒𝟕 miles. They take the same route and drive at constant speeds. Alan begins driving at 1:40 p.m. and arrives at City B at 4:15 p.m.

Margot’s trip from City A to City B can be described with the equation 𝒚 = 𝟔𝟒x, where y is the distance traveled in miles and 𝒙 is the time in minutes spent traveling.

Who gets from City A to City B faster?

Solution :

Alan's constant rate :

Time taken by Alan :

1.40 to 2.40 = 1 hour

2.40 to 3.40 = 1 hour

3.40 to 4.15 = 35 minutes

Total time take = 155 minutes.

Speed = Distance / time

Speed (or) Rate of change = 147/155

Margot's constant rate :

y = 64x

Rate of change of Margot = 64

Since Margot’s rate is faster, she will get to City B faster than Alan.

Problem 2 :

You have recently begun researching phone billing plans. Phone Company A charges a flat rate of $𝟕𝟓 a month. A flat rate means that your bill will be $𝟕𝟓 each month with no additional costs.

The billing plan for Phone Company B is a linear function of the number of texts that you send that month. That is, the total cost of the bill changes each month depending on how many texts you send.

The table below represents some inputs and the corresponding outputs that the function assigns.

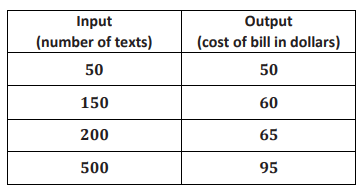
(i)  At what number of texts would the bill from each phone plan be the same?

(ii)  At what number of texts is Phone Company A the better choice?

(iii)  At what number of texts is Phone Company B the better choice?

Solution :

Charges of company A :

y = 75x ----(1)

Rate of change = 75

Rate of change of B :

Considering two points (50, 50) (150, 60).

m = (y₂ - y₁) / (x₂ - x₁)

m = (60 - 50) / (150 - 50)

m = 10 / 100

m = 1/10 ==> 0.1

By applying the value of m in y = mx + b, we get

y = 0.1x + b -----(2)

To get the value of b, we can apply the point (200, 65) in (2).

65 = 0.1(200) + b

65 = 20 + b

b = 65 - 20

b = 45

By applying the value of b in (1), we get

y = 0.1x + 45

(i)

(1) = (2)

75 = 0.1x + 45

75 - 45 = 0.1x

30 = 0.1x

x = 30/0.1

x = 300

After 𝟑𝟎𝟎 texts are sent, both companies would charge the same amount, $𝟕𝟓

(ii)  More than 𝟑𝟎𝟎 texts means that the bill from Phone Company B will be higher than Phone Company A.

(iii)  Less than 𝟑𝟎𝟎 texts means the bill from Phone Company A will be higher.

Problem 3 :

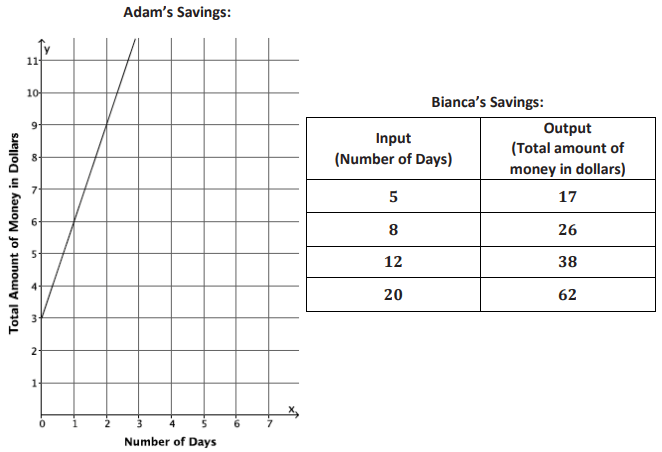
Two people, Adam and Bianca, are competing to see who can save the most money in one month. Use the table and the graph below to determine who will save the most money at the end of the month. State how much money each person had at the start of the competition. (Assume each is following a linear function in his or her saving habit.)

Solution :

Rate of change from graph :

(0, 3) and (1, 6)

m = (y₂ - y₁) / (x₂ - x₁)

m = (6 - 3) / (1 - 0)

m = 3

From the graph y-intercept is 3. So, at the beginning of the competition Adam has $3.

Rate of change from table :

(5, 17) (8, 26)

m = (26 - 17) / (8 - 5)

m = 9/3

m = 3

Equation in y-intercept form :

y = mx + b

y = 3x + b ----(1)

The line is passing through the point (12, 38).

38 = 3(12) + b

38 = 36 + b

38 - 36 = b

b = 2

So, at the beginning of the competition Bianca has $2.