FIND X AND Y INTERCEPTS OF A LINE

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

To find x and y-intercept of a line, we have two ways.

Method 1 :

(i) To find x-intercept, apply y = 0. Then write the coordinate as (x, 0).

(ii) To find y-intercept, apply x = 0. Then write the coordinate as (0, y).

Method 2 :

Convert the equation from standard form to intercept form.

(x/a) + (y/b) = 1

a = x-intercept and b = y-intercept

Here we see examples using the first method.

To get examples using second method, please click here

Find x and y intercepts from a equation of line

Find x and y intercepts of the lines given below.

Problem 1 :

x + 2y = 8

Solution:

x-intercept :

y = 0

x + 2y = 8

x + 0 = 8

x = 8

y-intercept :

x = 0

0 + 2y = 8

2y = 8

y = 4

So, x-intercept is 8 and y-intercept is 4.

Problem 2 :

3x - y = 6

Solution :

x-intercept :

y = 0

3x - y = 6

3x - 0 = 6

3x = 6

x = 2

y-intercept:

x = 0

0 - y = 6

-y = 6

y = -6

So, x-intercept is 2 and y-intercept is -6.

Problem 3 :

2x - 3y = 6

Solution :

x-intercept :

y = 0

2x - 3y = 6

2x - 0 = 6

2x = 6

x = 3

y-intercept :

x = 0

0 - 3y = 6

-3y = 6

y = -2

So, x-intercept is 3 and y-intercept is -2.

Problem 4 :

4x + 3y = 12

Solution :

x-intercept :

y = 0

4x + 3y = 12

4x + 0 = 12

4x = 12

x = 3

y-intercept :

x = 0

0 + 3y = 12

3y = 12

y = 4

So, x-intercept is 3 and y-intercept is 4.

Problem 5 :

x + y = 5

Solution :

x-intercept :

y = 0

x + y = 5

x + 0 = 5

x = 5

y-intercept :

x = 0

0 + y = 5

y = 5

So, x-intercept is 5 and y-intercept is 5.

Problem 6 :

x - y = - 5

Solution :

x-intercept :

y = 0

x - y = - 5

x - 0 = - 5

x = - 5

y-intercept :

x = 0

0 - y = - 5

-y = -5

y = 5

So, x-intercept is -5 and y-intercept is 5.

Problem 7 :

2x - y = - 4

Solution :

x-intercept :

y = 0

2x - y = - 4

2x - 0 = - 4

2x = -4

x = -2

y-intercept :

x = 0

0 - y = - 4

-y = - 4

y = 4

So, x-intercept is -2 and y-intercept is 4.

Problem 8 :

9x - 2y = 9

Solution :

x-intercept :

y = 0

9x - 2y = 9

9x - 0 = 9

9x = 9

x = 1

y-intercept :

x = 0

0 - 2y = 9

-2y = 9

y = -9/2

So, x-intercept is 1 and y-intercept is -9/2.

Problem 9 :

3x + 4y = -15

Solution :

x-intercept :

y = 0

3x + 4y = -15

3x + 0 = -15

3x = -15

x = -5

y-intercept :

x = 0

0 + 4y = -15

4y = -15

y = -15/4

So, x-intercept is -5 and y-intercept is -15/4.

Problem 10 :

The school band is selling sweatshirts and baseball caps raise $9000 to attend a band competition. Sweatshirts cost $25 each and base ball caps cost $10 each. The equation 25x + 10y = 9000 models this situation, where x is the number of sweatshirts sold and y is the number of baseball caps sold.

a) Find and interpret the intercepts

b) If 258 sweatshirts are sold, how many baseball caps are sold ?

c) Graph the equation. Find one more possible solutions in the context of the problem.

Solution :

25x + 10y = 9000

a) Interpreting intercepts :

x-intercept :

Put y = 0

Applying y = 0, we get

25x = 9000

x = 9000/25

x = 360

y-intercept :

Put x = 0

Applying x = 0, we get

10y = 9000

y = 9000/10

y = 900

Maximum number of sweatshirts sold is 360

Maximum number of baseball caps sold is 900

b) When x = 258

25(258) + 10y = 9000

6450 + 10y = 9000

10y = 9000 - 6450

10y = 2550

y = 2550/10

y = 255

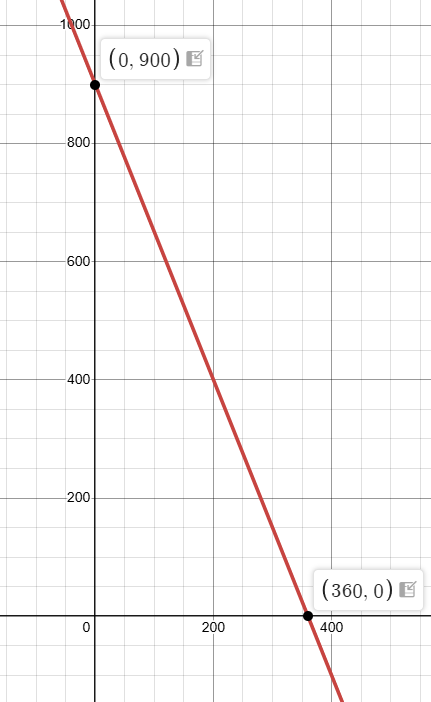
(200, 400) is one of the possible solution.

Problem 11 :

Your club is ordering enrollment gifts engraved with your club logo. Key chains cost $5 each. Wristbands cost $2 each. You have a budget of $150 for the gifts. The equation

5x + 2y = 150

models the total cost, where x is the number of key chains and y is the number of wristbands.

a. Graph the equation. Interpret the intercepts.

b. Your club decides to order 18 key chains. How many wristbands can you order?

Solution :

5x + 2y = 150

x-intercept :

Put y = 0

5x = 150

x = 150/5

x = 30

y-intercept :

Put x = 0

2y = 150

y = 150/2

y = 75

The maximum number of wristbands is 30

The maximum number of key chains is 75.

b) 5x + 2y = 150

When x = 18

5(18) + 2y = 150

90 + 2y = 150

2y = 150 - 90

2y = 60

y = 60/2

y = 30

So, the number of wristbands is 30.

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

FIND X AND Y INTERCEPTS OF A LINE

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling