DISTANCE BETWEEN TWO POINTS WORKSHEET

Problem 1 :

What is the approximate length of RS with endpoints R(2, 3) and S(4, -1)?                  Solution

Problem 2 :

What is the approximate length of AB with endpoints A(-3, 2) and B(1, -4)?             Solution

Problem 3 :

The endpoints of MN are M(-3, -9) and N(4, 8). What is the approximate length of MN?            Solution

Find the length of the segment. Round to the nearest tenth of a unit.

Problem 4 :

Solution

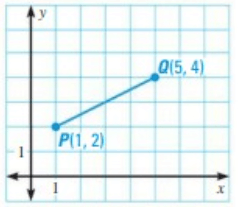
Problem 5 :

Solution

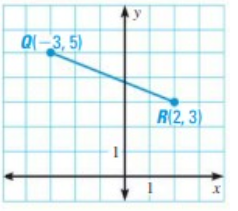
Problem 6 :

Solution

Problem 7 :

Calculate the perimeter of triangle ABC,

Solution

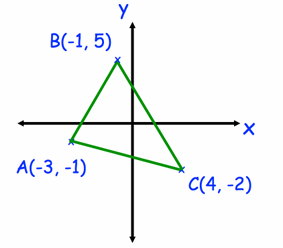
Problem 8 :

Two wolves spot a deer in a field. The positions of the animals are shown. Which wolf is closer to the deer?

Solution

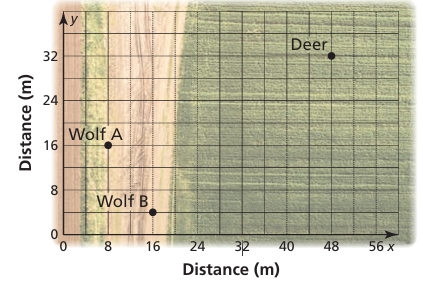
Problem 9 :

A theater is 3 miles east and 1 mile north of a bus stop. A museum is 4 miles west and 3 miles south of the bus stop. Estimate the distance between the theater and the museum

Solution

Problem 10 :

The endpoints of line segment AB are A(2x, y − 1) and B(y + 3, 3x + 1). The midpoint of line segment AB is M (−7/2, −8) . What is the length of line segment AB?

Solution

Use the given distance d between the two points to find the value of x or y.

Problem 1 :

(0, 3), (x, 5); d = 2√10

Solution

Problem 2 :

(-3, -1), (2, y); d = √41

Solution

Problem 3 :

(x, 7), (-4, 1); d = 6√2

Solution

Problem 4 :

(1, y), (8, 13); d = √74

Solution

Problem 5 :

Find the value of a, if the distance between the points A (–3, –14) and B (a, –5) is 9 units.

Solution

Problem 6 :

If the point A (2, – 4) is equidistant from P (3, 8) and Q (–10, y), find the values of y. Also find distance PQ.

Solution

Problem 7 :

The centre of a circle is (2a, a – 7). Find the values of a if the circle passes through the point (11, –9) and has diameter 10√2 units.

Solution

The vertices of a triangle are given. Classify the triangle as scalene, isosceles, or equilateral.

Problem 1 :

(-5, 0), (0, 6), (5, 0)

Solution

Problem 2 :

(0, -3), (0, 3), (3, 0)

Solution

Problem 3 :

(-2, 5), (1, -1), (4, 6)

Solution

Problem 4 :

(1, 4), (4, 1), (7, 4)

Solution

Problem 5 :

(-1, -6), (1, 1), (4, -5)

Solution

Problem 6 :

(-4, 3), (2, -1), (8, -1)

Solution

Problem 7 :

The coordinates of the vertices of triangle ABC are A(-5, 3), B(-1, -2) and C(2, 3). Show that triangle ABC is scalene.

Solution

Use the distance formula to classify triangle ABC, as either equilateral, isosceles or scalene :

Problem 1 :

A(3, -1), B(1, 8), C(-6, 1)

Solution

Problem 2 :

A(1, 0), B(3, 1), C(4, 5)

Solution

Problem 3 :

A(-1, 0), B(2, -2), C(4, 1)

Solution

Problem 4 :

A(√2, 0), B(-√2, 0), C(0, -√5)

Solution

Problem 5 :

A(√3, 1), B(-√3, 1), C(0, -2)

Solution

Problem 6 :

A(a, b), B(-a, b), C(0, 2)

Solution

Problem 1 :

Name the type of triangle formed by the points A(-5, 6), B(-4, -2) and C(7, 5).

Solution

Problem 1 :

Find the coordinates of the point Q on the x axis which lies on the perpendicular bisector of the line segment joining the points A(-5, -2) and B(4, -2). Name the type of triangle formed by the points Q, A and B.

Solution

Problem 3 :

If the vertices of triangle ABC are A(-2, 4), B(-2, 8) and C(-5, 6) then triangle ABC is classified as 

a) right        b)  scalene      c)  isosceles      d)  equilateral

Solution

Problem 4 :

Triangle ABC has vertices with A(x, 3), B(−3, −1), and C(−1, −4). Determine and state a value of x that would make triangle ABC a right triangle. Justify why ABC is a right triangle. [The use of the set of axes below is optional.]

Solution