CONVERTING BETWEEN SLOPE INTERCEPT AND STANDARD FORM

Convert from the given standard form of a linear equation to the slope-intercept form of a linear equation.

Problem 1 :

x + 5y = 5

Solution :

Given equation is in standard form :

x + 5y = 5

To convert this into slope intercept form, we have to isolate the variable y.

Subtract x on both sides

5y = -x + 5

Divide by 5 on sides.

y = (-x/5) + (5/5)

y = (-1/5)x + 1

It exactly matches with y = mx + b.

So, the slope = -1/5 and y-intercept = 1.

Problem 2 :

3x + 2y = 4

Solution :

Given equation is in standard form :

3x + 2y = 4

To convert this into slope intercept form, we have to isolate the variable y.

Subtract 3x on both sides

2y = -3x + 4

Divide by 2 on sides.

y = (-3x/2) + (4/2)

y = (-3/2)x + 2

It exactly matches with y = mx + b.

So, the slope = -3/2 and y-intercept = 2.

Problem 3 :

y = (-11x/10) - 1

Solution :

Given equation is in slope intercept form :

y = (-11x/10) - 1

y = (-11x/10) - (1/1)

LCM(10, 1) is 10.

y = (-11x/10)  - (10/10)

y = (-11x - 10)/10

Multiply by 10 on both sides.

10y = -11x - 10

Add 11x and 10 on both sides.

11x + 10y + 10 = 0

So, the standard form is 11x + 10y + 10 = 0.

Problem 4 :

y = -2x - 9

Solution :

Slope intercept form :

y = -2x - 9

Add 2x on both sides.

2x + y = -9

Add 9 on both sides.

2x + y + 9 = 0

So, the standard form is 2x + y + 9 = 0.

Problem 5 :

You have $6 to spend on apples and bananas.

(a) Graph the equation 1.5x + 0.6y = 6, where x is the number of pounds of apples and y is the number of pounds of bananas.

(b) Interpret the intercepts.

Solution :

a)  1.5x + 0.6y = 6

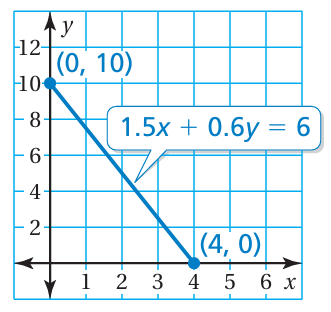
b)  The x-intercept shows that you can buy 4 pounds of apples if you don’t buy any bananas. The y-intercept shows that you can buy 10 pounds of bananas if you don’t buy any apples.

Problem 6 :

Define two variables for the verbal model. Write an equation in slope-intercept form that relates the variables. Graph the equation.

a)  ($2.00/pound) ⋅ Pounds of peaches + ($1.50/pound) ⋅ Pounds of apples = $15

b) (16 miles/hour) ⋅ Hours biked + (2 miles/hour) ⋅ Hours walked = 32 miles

Solution :

a)  ($2.00/pound) ⋅ Pounds of peaches + ($1.50/pound) ⋅ Pounds of apples = $15

Let x be the pound of peaches and y be the pounds of apples.

2x + 1.5y = 15

To graph the equation, we find x-intercept and y-intercept.

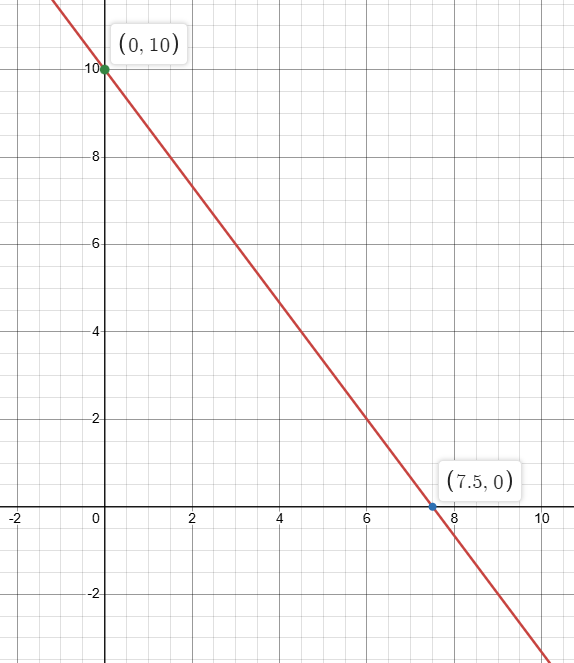
b) (16 miles/hour) ⋅ Hours biked + (2 miles/hour) ⋅ Hours walked = 32 miles

Let x be the number of hours biked and y be the number of hours walked.

16x + 2y = 32

To graph the equation, we find x-intercept and y-intercept.

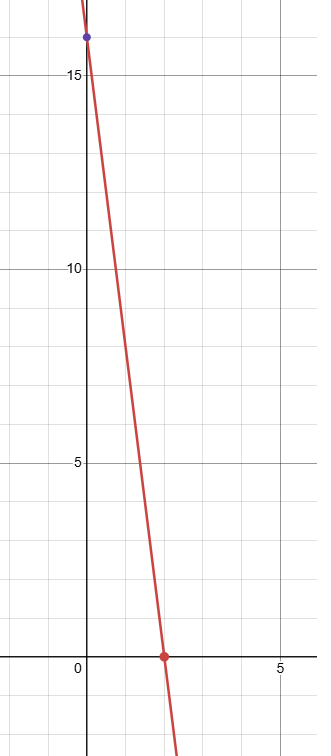
Problem 7 :

A charm bracelet costs $65, plus $25 for each charm.

a. Write an equation in standard form that represents the total cost of the bracelet.

b. How much does the bracelet shown cost?

Solution :

Let x be the cost of each charm and y be the total cost.

a) y = 65 + 25x

b) Number of charms = 13

To find the total cost, we apply x = 13

y = 65 + 25(13)

y = 65 + 325

y = 390

So, the total cost is $390.

Related pages

• More problems on standard form to slope intercept form
• More problems on slope intercept form to standard form