CONVERTING FROM STANDARD FORM TO SLOPE INTERCEPT FORM
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Standard Form
The linear equation in two variables in standard form will be
ax + by + c = 0
a = coefficient of x
b = coefficient of y
c = constant
Slope Intercept Form
The linear equation in two variables in slope intercept form will be
y = mx + b
m = slope
b = y-intercept
Convert from the given standard form of a linear equation to the slope-intercept form of a linear equation.
Problem 1 :
x + 5y = 5
Solution :
Given equation is in standard form :
x + 5y = 5
To convert this into slope intercept form, we have to isolate the variable y.
Subtract x on both sides
5y = -x + 5
Divide by 5 on sides.
y = (-x/5) + (5/5)
y = (-1/5)x + 1
It exactly matches with y = mx + b.
So, the slope = -1/5 and y-intercept = 1.
Problem 2 :
3x + 2y = 4
Solution :
Given equation is in standard form :
3x + 2y = 4
To convert this into slope intercept form, we have to isolate the variable y.
Subtract 3x on both sides
2y = -3x + 4
Divide by 2 on sides.
y = (-3x/2) + (4/2)
y = (-3/2)x + 2
It exactly matches with y = mx + b.
So, the slope = -3/2 and y-intercept = 2.
Problem 3 :
2x + y = 4
Solution :
Given equation is in standard form :
2x + y = 4
To convert this into slope intercept form, we have to isolate the variable y.
Subtract 2x on both sides
y = -2x + 4
It exactly matches with y = mx + b.
So, the slope = -2 and y-intercept = 4.
Problem 4 :
4x – 2y = 6
Solution :
Given equation is in standard form :
4x – 2y = 6
To convert this into slope intercept form, we have to isolate the variable y.
Add 2y and subtract 6 on both sides.
4x - 6 = 2y
2y = 4x - 6
Divide by 2 on both sides.
y = (4x/2) - (6/2)
y = 2x - 3
It exactly matches with y = mx + b.
So, the slope = 2 and y-intercept = -3.
Problem 5 :
8x – 4y = 16
Solution :
Given equation is in standard form :
8x – 4y = 16
To convert this into slope intercept form, we have to isolate the variable y.
Add 2y and subtract 6 on both sides.
4x - 6 = 2y
2y = 4x - 6
Divide by 2 on both sides.
y = (4x/2) - (6/2)
y = 2x - 3
It exactly matches with y = mx + b.
So, the slope = 2 and y-intercept = -3.
Problem 6 :
3x + 4y = 4
Solution :
3x + 4y = 4
Subtract 3x on both sides.
4y = -3x + 4
Divide by 4 on both sides.
y = (-3/4)x + (4/4)
y = (-3/4)x + 1
Slope = -3/4 and y-intercept = 1
Problem 7 :
9x – 4y = -16
Solution :
Add 4y on both sides.
9x = -16x + 4y
Add 16 on both sides.
9x + 16 = 4y
4y = 9x + 16
Divide by 4 on both sides.
y = (9/4) x + (16/4)
y = (9/4) x + 4
Slope = 9/4 and y-intercept = 4.
Problem 8 :
2x – 5y = 10
Solution :
2x – 5y = 10
Add 5y on both sides.
2x = 5y +10
Subtract 10 on both sides.
2x - 10 = 5y
Divide by 5 on both sides.
y = (2/5)x - (10/5)
y = (2/5)x - 2
Slope = 2/5 and y-intercept = -2
Problem 9 :
3x + 5y = -25
Solution :
3x + 5y = -25
Subtract 3x on both sides.
5y = -3x - 25
Divide by 5.
y = (-3/5)x - (25/5)
y = (-3/5)x - 5
Problem 10 :
7x – y = 4
Solution :
7x – y = 4
Add y on both sides.
7x = y + 4
Subtract 4 on both sides.
7x - 4 = y
y = 7x - 4
Slope = 7 and y-intercept = -4.
Problem 11 :
Write a linear function in slope intercept form where f with the values f(0) = 10 and f(6) = 34.
Solution :
f(0) = 10 and f(6) = 34
(0, 10) and (6, 34) are the two points on the line
Slope = (y2 - y1) / (x2 - x1)
= (34 - 10) / (6 - 0)
= 24/6
= 4
When x = 0, y = 10. Then y-intercept (b) = 10
y = mx + b
y = 4x + 10
Problem 12 :
Describe and correct the error in writing an equation of the line with a slope of 2 and a y-intercept of 7.
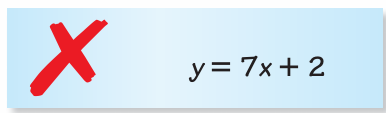
Solution :
Comparing the given equation with y = mx + b
y = 7x + 2
Here slope = 7 and y-intercept = 2
The erros is, given that slope is 2 and y-intercept is 7.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling