CLASSIFYING TYPES OF DISCONTINIUITY PRACTICE PROBLEMS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Discuss the continuity. If a discontinuity exists, then describe the type of discontinuity and its physical feature on a graph.
Problem 1 :
Problem 2 :
Problem 3 :
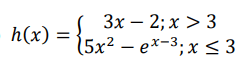
Problem 4 :
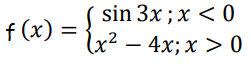
Problem 5 :

Problem 6 :
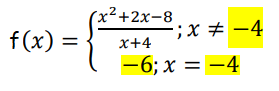
Answer Key
1) Removable discontinuity at x = 3 or hole is at x = 3.
Non removable discontinuity is at x = 1.
2) Non removable discontinuity is at x = 3 or jump discontinuity is at x = 3.
3) Non removable discontinuity is at x = 3 or jump discontinuity is at x = 3.
4) Removable discontinuity is at x = 0 or hole is at x = 0.
5) Removable discontinuity is at x = 1 or hole is at x = 1.
6) The function is continuous.
For each function identify the type of discontinuity and where it is located.
Problem 1 :
Problem 2 :
Problem 3 :
f(x) = x3 - 4x
Problem 4 :
Problem 5 :
f(x) = sec 2x for 0 ≤ x ≤ 2π
Problem 6 :
Problem 7 :
Problem 8 :
Problem 9 :
Problem 10 :
f(x) = csc (x/2) for 0 ≤ x ≤ 2π
Problem 11 :
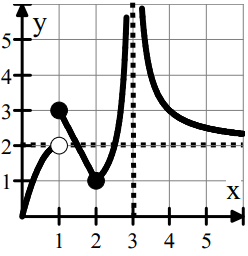
The graph of the function 𝑓(𝑥) is shown to the right: Which of the following statements is true about 𝑓?
I. 𝑓 is undefined at 𝑥 = 1.
II. 𝑓 is defined but not continuous at 𝑥 = 2.
III. 𝑓 is defined and continuous at 𝑥 = 3.
(A) Only I (B) Only II (C) I and II
(D) I and III (E) None of the statements are true.
Problem 12 :
The function f(x) has removable discontinuity at
(A) x = -2 only (B) x = 0 only (C) x = 1 only
(D) x = -2 and x = 0 only
(E) f(x) has no removable discontinuities
Problem 13 :
On what intervals is f(x) continuous ?
a) [-3, -2] U [-2, 0] U [0, 2.5] b) [-3, -2] U (-2, 0] U [0, 2.5]
c) [-3, -2] U (-2, 0] U (0, 2.5] d) [-3, -2] U [-2, 0] U (0, 2.5]
Problem 14 :
The function has jump discontinuity is at ?
Answer Key
1) non removable discontinuity at x = -1. Vertical asymptote is at x = -1.
2) Removable discontinuity at x, non removable discontinuity at x = -3.
3) the function is continuous for all real values .
4) removable discontinuity or hole at x = -3
5) non removable discontinuities at x = π/4, 3π/4, 5π/4 and 7π/4.
6) Removable discontinuity at x = -2, Non removable discontinuity or hole is at x = 4.
7) Removable discontinuity at x = 5, Non removable discontinuity or hole is at x = 2.
8) there is non removable discontinuity is at x = 5/2.
9) the function is continuous for all real values.
10) Vertical asymptotes are at x = 0, 2π
11) none of the statement are true, E
12) option E is correct.
13) Between 0 to 2.5, it is continuous. So, option c is correct.
14) At x = -2 and at x = 0, the function has jump discontinuities.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling