CLASSIFYING TRIANGLES WORKSHEET

Please visit the below link

How to Classify Triangles Based on Side Measures

How to Classify Triangles Based on Angles Measures

Problem 1 :

A triangle cannot have unequal side measures.

A)  True     B)  False

Solution :

This is a false statement.

Because all three sides of the scalene triangle are unequal.

Problem 2 :

Name the triangle by observing its side lengths.

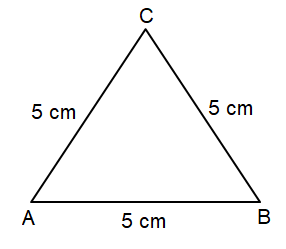
Solution :

By observing the figure,

AB = BC = AC = 5 cm

Since all the sides are equal in length, it is an Equilateral Triangle.

Problem 3 :

Identify the triangle based on indicated sides.

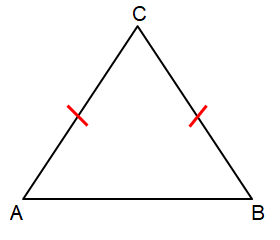
Solution :

By observing the figure,

AC and BC are congruent. It is represented by a single hash mark on each side.

So, it is an Isosceles Triangle.

Problem 4 :

Name the following triangles based on their sides and angles.

a)

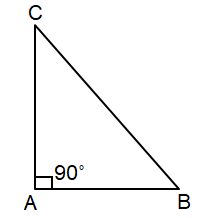
Solution :

By observing the figure, <A = 90˚

Since one of the angles is 90˚, it is a Right Angle Triangle.

b)

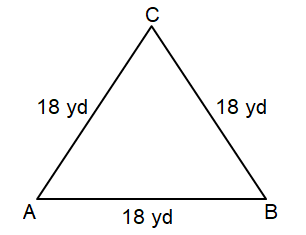
Solution :

By observing the figure,

AB = BC = AC = 18 yd

Since all the sides are equal in length, it is an Equilateral Triangle.

c)

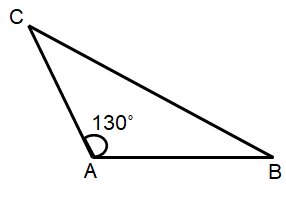
Solution :

By observing the figure, <A = 130˚

Since <A is greater than 130˚, it is an Obtuse Angle Triangle.

Problem 5 :

Identify the triangle based on the angles.

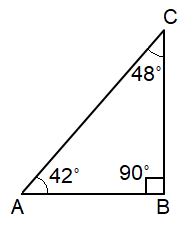
Solution :

By observing the figure, <B = 90˚

Since one of the angles is 90˚, it is a Right Angle Triangle.

Problem 6 :

Name the triangle by looking into its side measures.

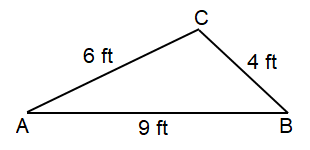
Solution :

By observing the figure,

AB = 9 ft, BC = 4 ft, and, AC = 6 ft

Since all the sides are different in length, it is an Scalene Triangle.

Problem 7 :

A triangle having two sides of equal measures is known as _----------- triangle.

Solution :

A triangle having two sides of equal measures is known as Isosceles triangle.

Problem 8 :

The given triangle is :

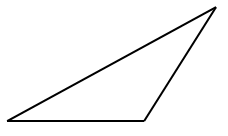
A)  Acute Triangle   B)  Obtuse Triangle  C) Right Triangle

Solution :

By observing the figure,

Since one of the angles is greater than 90˚, it is an Obtuse Angle Triangle.

Problem 9 :

What is an Obtuse Angled Triangle ?

Solution :

If one of the angles is greater than 90˚, then the triangle is classified as an Obtuse Angle Triangle.

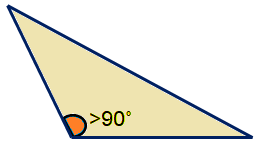
Problem 10 :

A triangle having all angles lesser than 90 degree is known as Right Angled Triangle.

A)  Yes     B)  No

Solution :

No, It is a false Statement.

If all the angles of the triangle are all less than  90˚, then the triangle is classified as an Acute Angle Triangle.

Classify △ABC by its sides. Then determine whether it is a right triangle.

Problem 11 :

A(2, 3), B(6, 3), C(2, 7)

Solution :

Distatnce between two points = √(x₂ - x₁)² + (y₂ - y₁)²

Length of AB = √(6 - 2)² + (3 - 3)²

= √4² + 0²

= 4

Length of BC = √(2 - 6)² + (7 - 3)²

= √(-4)² + 4²

= √(16 + 16)

= √32

Length of CA = √(2 - 2)² + (7 - 3)²

= √0² + 4²

= √16

= 4

BC² = AB² + BC²

32 = 4² + 4²

32 = 16 + 16

32 = 32

It is a right triangle.

Problem 12 :

A(3, 3), B(6, 9), C(6, −3)

Solution :

Distatnce between two points = √(x₂ - x₁)² + (y₂ - y₁)²

Length of AB = √(6 - 3)² + (9 - 3)²

= √3² + 6²

= √9 + 36

= √45

Length of BC = √(6 - 6)² + (-3 - 9)²

= √0² + (-12)²

= √144

= 12

Length of CA = √(6 - 3)² + (-3 - 3)²

= √3² + (-6)²

= √9 + 36

= √45

Since two sides are equal, it must be isosceles triangle.

Problem 13 :

A(1, 9), B(4, 8), C(2, 5)

Solution :

Distatnce between two points = √(x₂ - x₁)² + (y₂ - y₁)²

Length of AB = √(4 - 1)² + (8 - 9)²

= √3² + (-1)²

= √9 + 1

= √10

Length of BC = √(2 - 4)² + (5 - 8)²

= √(-2)² + (-3)²

= √(4 + 9)

= √13

Length of CA = √(2 - 1)² + (5 - 9)²

= √1² + (-4)²

= √1 + 16

= √17

All three sides are different, so it must be a scalane triangle.

Problem 14 :

A(−2, 3), B(0, −3), C(3, −2)

Solution :

Distatnce between two points = √(x₂ - x₁)² + (y₂ - y₁)²

Length of AB = √(0 + 2)² + (-3 - 3)²

= √2² + (-6)²

= √4 + 36

= √40

Length of BC = √(3 - 0)² + (-2 + 3)²

= √3² + 1²

= √9 + 1

= √10

Length of CA = √(3 + 2)² + (-2 - 3)²

= √5² + (-5)²

= √25 + 25

= √50

CA² = AB² + BC²

√50² = √40² + √10²

50 = 40 + 10

50 = 50

It is a right triangle.

Problem 15 :

The measure of one acute angle is 5 times the measure of the other acute angle  find the measure of each acute angle in the right triangle.

Solution :

One of the angles in a triangle is right angle. Let x be one acute angle, then other acute angle will be 5x.

The angles are 90, x and 5x

Sum of angles of triangle = 180

90 + x + 5x = 180

6x = 180 - 90

6x = 90

x = 90/6

x = 15

5x = 5(15) ==> 75

So, the acute angles are 15 and 75.