CLASSIFYING TRIANGLES BASED ON SIDE MEASURES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
On the basis of the length of the sides, triangles are classified into three categories.
- Scalene Triangle
- Isosceles Triangle
- Equilateral Triangle
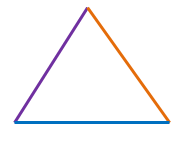
Scalene Triangle
If all the sides are different in length, then the triangle is Scalene Triangle.
Isosceles Triangle
If two sides are the same in length, then the triangle is Isosceles Triangle.
Equilateral Triangle
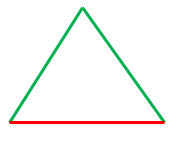
If all the sides are the same in length, then the triangle is Equilateral Triangle.

Identify each triangle based on sides.
Problem 1 :
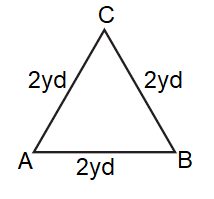
Solution :
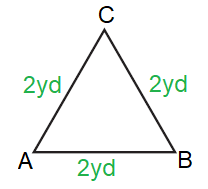
By observing the figure,
AB = BC = AC = 2yd
Since all the sides are equal in length, it is an
Equilateral Triangle
Problem 2 :
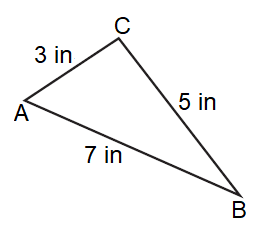
Solution :
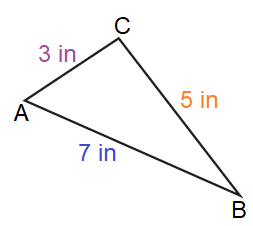
By observing the figure,
AB = 7 in, BC = 5 in, and, AC = 3 in
Since all the sides are different in length, it is an
Scalene Triangle
Problem 3 :
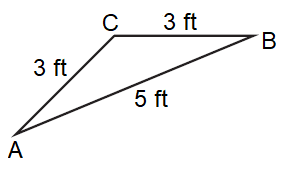
Solution :
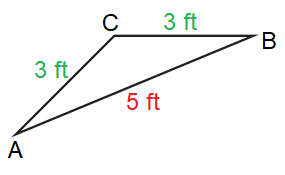
By observing the figure,
AB = 5 ft, BC = 3 ft, and, AC = 3 ft
Since the two sides are the same in length, it is an
Isosceles Triangle
Problem 4 :
Solution :
By observing the figure,
AB = 3 in, BC = 2 in, and, AC = 2 in
Since the two sides are the same in length, it is an
Isosceles Triangle
Problem 5 :
Solution :
By observing the figure,
AB = BC = AC = 4 ft
Since all the sides are equal in length, it is an
Equilateral Triangle
Problem 6 :
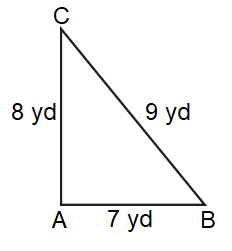
Solution :
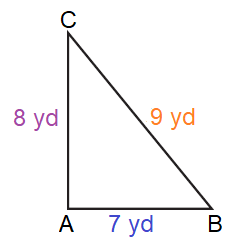
By observing the figure,
AB = 7 yd, BC = 9 yd, and, AC = 8 yd
Since all the sides are different in length, it is an
Scalene Triangle
Problem 7 :
Find the value of x. Then classify each triangle.
a. Flag of Jamaica
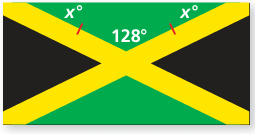
b. Flag of Cuba

Solution :
a) Flag of Jamica :
Sum of interior angles of triangle = 180
128 + x + x = 180
128 + 2x = 180
2x = 180 - 128
2x = 52
x = 52/2
x = 26
The angle measures are 26, 26 and 128. Since two angle measures are equal, then it is isosceles triangle.
b) Flag of Cuba
x + x + 60 = 180
2x + 60 = 180
2x = 180 - 60
2x = 120
x = 120/2
x = 60
The angle measures are 60, 60, and 60. Since all angle measures are equal, then it is equilateral triangle.
Problem 8 :
An airplane leaves from Miami and travels around the Bermuda Triangle. What is the value of x?
a) 26.8 b) 27.2 c) 54 d) 64
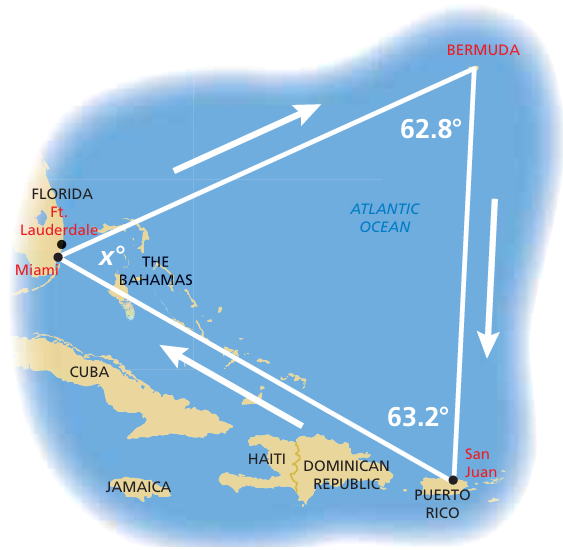
Solution :
The angles are x, 62.8 and 63.2
Sum of interior angles = 180
x + 62.8 + 63.2 = 180
x + 126 = 180
x = 180 - 126
x = 54
Since the angle measures are different, then it must be scalene triangle.
Problem 9 :
Shown below is an isosceles triangle.
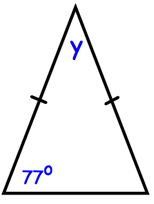
Work out the size of the angle marked y.
Solution :
y + 77 + 77 = 180
y + 154 = 180
y = 180 - 154
y = 26
So, the missing angle measure is 26. Since the two angle measures are equal, it must be a isosceles triangle.
Problem 10 :
In an acute triangle, the measures of two angles are 50° and 60°. What is the measure of the third angle?
Solution :
Two angle measures are 50° and 60°. Let x be the third angle.
x + 50 + 60 = 180
x + 110 = 180
x = 180 - 110
x = 70
So, the third angle measure is 70 degree.
Problem 11 :
In an obtuse triangle, the measures of two angles are 120° and 10°. What is the measure of the third angle?
Solution :
Two angle measures are 120° and 10°. Let x be the third angle.
x + 120 + 10 = 180
x + 130 = 180
x = 180 - 130
x = 50
So, the third angle measure is 50 degree.
Problem 12 :
One acute angle of a right triangle measures 35°. What is the measure of the other acute angle?
Solution :
Given that is a right triangle. The two angle measures are 90° and 35°. Let x be the third angle.
x + 90 + 35 = 180
x + 125 = 180
x = 180 - 125
x = 55
So, the other acute angle is 55.
Problem 13 :
In a triangle ABC, ∠A = 2X + 7, ∠B = 5X - 15, and ∠C = 6X. What is the value of x and what are the measures of angles A, B, and C?
Solution :
∠A + ∠B + ∠C = 180
2x + 7 + 5x - 15 + 6x = 180
2x + 5x + 6x + 7 - 15 = 180
13x - 8 = 180
13x = 180 + 8
13x = 188
x = 188/13
x = 14.4
|
∠A = 2(14.4) + 7 = 28.8 + 7 = 35.8 |
∠B = 5(14.4) - 15 = 72 - 15 = 57 |
∠C = 6(14.4) = 86.4 |
So, the angle measures are 35.8, 57 and 86.4
Problem 14 :
Below are 3 straight lines.
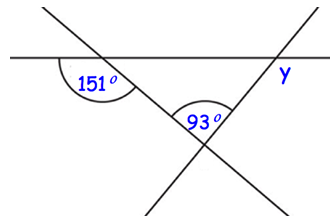
Below are 3 straight lines.
Solution :
Let x be the missing angle inside the triangle.
151 + x = 180
x = 180 - 151
x = 29
y = 180 - (93 + 29)
y = 180 - 122
y = 58
So, the value of y is 58.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling