CALCULUS OPTIOMIZATION PRACTICE PROBLEMS WORKSHEET

Problem 1 :

If a business employs x workers to manufacture furniture then the profit made by the business given by

P(x) = -3x³ + 6084x - 5000 dollars per week

a) How many employees should the business have to maximize the profit ?

b) What is the maximum profit ?

Solution

Problem 2 :

Two numbers have the sum of 10. What is the minimum value that the sum of their cubes could be ?

Solution

Problem 3 :

What is the least possible value of the sum of a positive number and its reciprocal ?

Solution

Problem 4 :

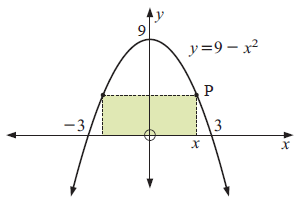
A rectangle sits on the x-axis under the graph of y = 9 - x²

a) Find the coordinate of P.

b) Write down a formula for the area of the rectangle in terms of x.

c)  Find the maximum possible area of the rectangle.

Solution

Problem 5 :

A beam with a rectangular cross section is to be cut from a log of diameter of 1 m.

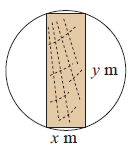
The strength of the beam varies in proportion to the width and to the square of the depth.

a) If the beam is x m and y m deep, write down the equation connecting x and y.

b) The strength S of the beam is given by width times the square of depth. Write down the formula for S in terms of x only.

c)  Find the dimensions of the strongest possible beam that can be cut from the log.

Solution