CALCULUS OPTIMIZATION PROBLEMS

Problem 1 :

If a business employs x workers to manufacture furniture then the profit made by the business given by

P(x) = -3x³ + 6084x - 5000 dollars per week

a) How many employees should the business have to maximize the profit ?

b) What is the maximum profit ?

Solution :

P(x) = -3x³ + 6084x - 5000

P'(x) = -3(3x²) + 6084(1) - 0

P'(x) = -9x² + 6084

P'(x) = 0

-9x² + 6084 = 0

-9x² = -6084

x² = 6084/9

x² = 676

x = 26

Applying the value of x in the second derivative.

P''(x) = -9(2x) + 0

P''(x) = -18x

Applying x = 26

P''(26) = -18(26) < 0 maximum at x = 26

a) So, the number of employees should have in the business is 26.

b) Maximum profit, 

P(26) = -3(26)³ + 6084(26) - 5000

= -3(17576) + 158184 - 5000

= -52728  + 158184 - 5000

= 100456

Problem 2 :

Two numbers have the sum of 10. What is the minimum value that the sum of their cubes could be ?

Solution :

Let x and 10 - x be two numbers,

Let the required function be f(x).

f(x) = x³ + (10 - x)³

f'(x) = 3x² + 3(10 - x)² (-1)

f'(x) = 3x² - 3(10 - x)²

f'(x) = 0

3x² - 3(10 - x)² = 0

x² = (10 - x)²

x = 10 - x

x + x = 10

2x = 10

x = 5

Applying the value of x in the second derivative.

f''(x) = 6x + 6(10 - x)

= 6(5) + 6(10 - 5) > 0

Minimum at x = 5.

Minimum value = x³ + (10 - x)³

= 5³ + (10 - 5)³

= 125 + 125

= 250

Problem 3 :

What is the least possible value of the sum of a positive number and its reciprocal ?

Solution :

Least value means minimum value. Let x be the required number.

Let f(x) be the required function and it will be

f(x) = x + 1/x 

f'(x) = 1 - 1/x²

1 - 1/x² = 0

1 = 1/x²

x² = 1

x = 1 and -1

Since it is positive number -1 to be ignored.

Applying x = 1 in the second derivative.

f'(x) = 1 - 1/x²

f''(x) = 0 + 1/x³

f''(1) = 1/1³  ==> 1

To find the least value, we can apply x = 1 in the function f(x).

f(x) = 1 + 1/1 

= 2

So, the least value is 2.

Problem 4 :

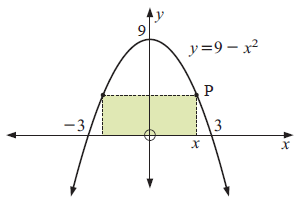
A rectangle sits on the x-axis under the graph of y = 9 - x²

a) Find the coordinate of P.

b) Write down a formula for the area of the rectangle in terms of x.

c)  Find the maximum possible area of the rectangle.

Solution :

a) The coordinate P is (x, 9 - x²)

b)  Area of the shaded region.

Area of the rectangle = length x width

length = x + x ==> 2x

width = 9 - x²

= 2x (9 - x²)

A(x) = 18x - 2x³

c) Maximum area :

A(x) = 18x - 2x³

A'(x) = 18(1) - 2(3x²)

= 18 - 6x²

A'(x) = 0

18 - 6x² = 0

6x² = 18

x² = 3

x = √3 and -√3

A' (x) = 18 - 6x²

A'' (x) = 0 - 12x

= -12x

We will get maximum possible area when x = √3

Finding area of the rectangle :

A(√3) = 18√3 - 2(√3)³

= 18√3 - 6√3

= 12√3

So, the maximum area is 12√3 square units.

Problem 4 :

A beam with a rectangular cross section is to be cut from a log of diameter of 1 m.

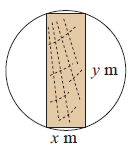
The strength of the beam varies in proportion to the width and to the square of the depth.

a) If the beam is x m and y m deep, write down the equation connecting x and y.

b) The strength S of the beam is given by width times the square of depth. Write down the formula for S in terms of x only.

c)  Find the dimensions of the strongest possible beam that can be cut from the log.

Solution :

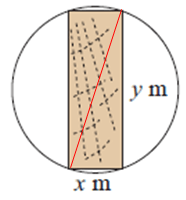
a) By connecting points shown above, the red line is the diameter of the sphere. Using Pythagorean theorem,

x² + y² = 1²

x² + y² = 1

b) Strength =  xy²

From x² + y² = 1, y² = 1 - x²

Applying the value of y², we get

Strength = x (1 - x²)

c)  Strongest means maximum.

f(x) = x (1 - x²)

f'(x) = x(0 - 2x) + (1 - x²)(1)

= -2x² + 1 - x²

f'(x) = -3x² + 1

f'(x) = 0

-3x² + 1 = 0

x² = 1/3

x = 1/√3

x = 0.577

Applying the value of x in second derivative, we get

f'(x) = -6x + 0

= -6x

f''(0.577) = -6(0.577)

= -3.46 < 0 maximum

y² = 1 - x²

= 1 - (0.577)²

= 1 - 0.3329

y² = 0.6670

y = 0.816

So, the dimension is 0.577 m and 0.816 m.