APPLICATION PROBLEMS OF PERFECT SQUARE NUMBERS WORKSHEET

Problem 1 :

The smallest number added to 680621 to make the sum a perfect square is :

(a) 4     (b)  5    (c)  6   (d) 8

Solution

Problem 2 :

What is the smallest number to be added to 1000 to make the resulting figure as perfect square.

Solution

Problem 3 :

If √1369 + √(0.0615) + x = 37.25, then x is equal to 

(a) 10^-1         (b) 10^-2           (c) 10^-3         (d) None

Solution

Problem 4 :

The sum of two numbers is 22 and the sum of their square is 404, then the product of the numbers is 

Solution

Problem 5 :

Solution

Problem 6 :

If y = 5, then what is the value of 10y √y³ - y² ?

a) 50 √2     b)  100   c)  200√5    d)  500

Solution

Problem 7 :

If 52/x = √(169/289), then the value of x is

a) 52     b)  58   c)  62    d)  68

Solution

Problem 8 :

If √1369 + √(0.0615 + x) = 37.25, then x is equal to 

a) 10^-1        b)  10^-2       c)  10^-3      d) None

Solution

Problem 9 :

If √(0.04 x 0.4 x a)  = 0.004 x 0.4 x √b, then a / b is :

a) 16 x 10^-3        b)  16 x 10^-4       c)  16 x 10^-5      d) None

Solution

Problem 10 :

If 28√x + 1426 = 3/4 of 2872

a) 576        b)  676       c)  1296      d) 144

Solution

Problem 1 :

What is the smallest number to be subtracted from 549162 in order to make it a perfect square?

a)   28     b)   36     c)   62     d)   81

Solution

Problem 2 :

What is the least number which should be subtracted from 0.000326 to make it a perfect square?

a)   0.000002   b)   0.000004    c)   0.02    d)   0.04

Solution

Problem 3 :

A general wishes to draw up his 36581 soldiers in the form of a solid square. After arranging them, he found that some of them are left over. How many are left ?

(a)  65     (b) 81   (c)  100   (d) None

Solution

Problem 4 :

Find the smallest number that must be subtracted to 1780 to make it a perfect square.

Solution

Problem 5 :

Find the least number which must be subtracted from 3250 so as to get a perfect square

Solution

Problem 6 :

What is the least number should be subtracted from 1385 to get a perfect square ? Also find the square root of the perfect square.

Solution

Problem 7 :

Find the least number which must be subtracted from each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.

(a) 402     (b) 1989    (c) 3250    (d) 825

Solution

Problem 8 :

Find the least number which must be added to each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.

(a) 525        (b) 1750      (c) 1825

Solution

Problem 1 :

The least number by which 294 must be multiplied to make it a perfect square, is

a)   2        b)   3        c)   6    d)   24

Solution

Problem 2 :

Find the smallest number by which 5808 should be multiplied so that the product becomes a perfect square.

a)   2      b)   3       c)   7        d)   11

Solution

Problem 3 :

By which least number should 22050 be multiplied such that the result is a perfect square.

Solution

Problem 4 :

Find the smallest common multiple of 48, 72 and 32 that is a perfect cube.

Solution

Problem 5 :

What is the smallest common multiple of 72 and 108 that is a perfect square ?

Solution

Problem 6 :

By which least number should 4375 be multiplied such that the result is a perfect square ?

Solution

Problem 7 :

By which least number should 72000 be multiplied such that the result is a perfect square ?

Solution

Problem 8 :

Find the smallest number by which 375 must be multiplied to obtain a perfect cube.

Solution

Problem 9 :

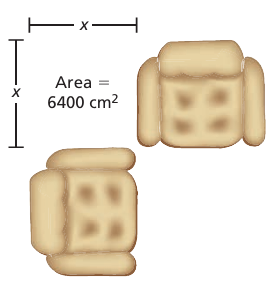
You have 275 square inches of wrapping paper. Do you have enough wrapping paper to wrap the gift box shown? Explain.

Solution

Problem 10 :

A cube-shaped end table has a volume of 216,000 cubic centimeters. Does the end table fit in the corner shown? Justify your answer

Solution

Problem 1 :

The least number, by which 1470 must be divided to get a number which is a perfect square, is:

a)   5    b)   6    c)   15     d)   30

Solution

Problem 2 :

By which least number should 3087 be divided in order to get a perfect square?

Solution

Problem 3 :

A man plants 15376 apple trees in his garden and arranges them so that there are as many rows as there are apples trees in each row. The number of rows is 

(a)  124   (b) 126  (c) 134   (d) 144

Solution

Problem 4 :

If 52/x = √(169/289), the value of x is 

(a) 52   (b) 58   (c) 62   (d) 68

Solution

Problem 5 :

The least number by which 1470 must be divided to get a number which is perfect square is :

a)  5        (b) 6       (c) 15      (d) 30

Solution

Problem 6 :

By what least number should 735 be multiplied so that the product is a perfect square. Find the square root of the product so obtained.

Solution

Problem 7 :

A general wishing to draw his 64029 men in the form of a square found that he had 20 men extra. Find the number of men in the front row.

Solution

Problem 8 :

Simplify :

√0.0441/√0.000441

Solution

Problem 9 :

The smallest number to be multiplied by 72 to make it a perfect square is

a) 2      b) 3      c) 5

Solution

Problem 10 :

The smallest number to be divided by 125 to make it a perfect square is

a) 25       b) 5      c) 1

Solution

Problem 11 :

The smallest number to be multiplied by 292 to make it a perfect square is

a) 2      b) 3      c) 73

Solution

Problem 12 :

The least number to be divided by 52 to make it a perfect square is

a) 13      b) 4     c) 2

Solution