WRITING SYSTEM OF INEQUALITIES FROM A GRAPH

Problem 1 :

What system of inequalities best represents the graph shown below?

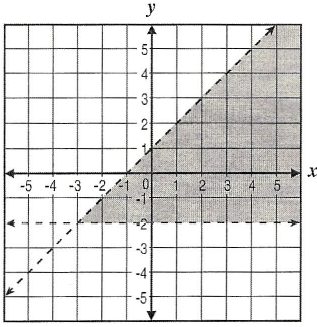
A)  y > - 2 and y > x +1

B)  y > - 2 and y < x + 1

C)  y < - 2 and y > x +1

D)  y < - 2 and y < x + 1

Solution :

In the graph, we see one raising line and one horizontal line.

Raising line passes through the points (-1, 0) and (0, 1).

Slope of the raising line :

Slope (m) = (y₂ - y₁)/(x₂ - x₁)

= (1 - 0) / (0 + 1)

= 1/1

= 1

y-intercept = 1

Equation of the raising line :

y = mx + b

y = 1x + 1

y = x + 1

Equation of horizontal line :

y = -2

When we observe the shaded region, it is above -2. So it should be greater(>) than -2. We can clearly reject options C and D.

Selecting one of the points ex : (2, 1) from the shaded region and applying it.

So, option B is correct.

Problem 2 :

Which system of linear inequalities is represented by this graph?

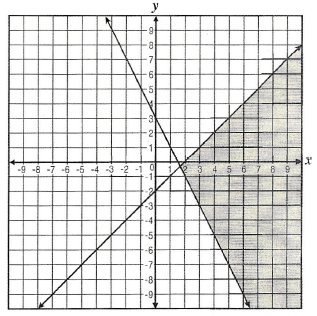
A) y ≥ (1/2)x + 3 and y ≥ x - 2

B) y ≥ 2x + 3 and y ≤ x - 2

C) 2x - y ≥ 3 and x + y ≤ 2

D) 2x + y ≥ 3 and x - y ≥ 2

Solution :

In the given graph, we have one raising line and one falling line.

Raising line has -2 as y-intercept and it passes through (0, -2) and (3, 1).

Slope of raising line :

m = (y₂ - y₁)/(x₂ - x₁)

= (1 + 2) / (3 - 0)

= 3/3

= 1

y-intercept = -2

Equation of raising line :

y = mx + b 

y = 1x - 2

Any two points from the falling line are (0, 3) and (1, 1) and it has the y-intercept is 3.

Slope (m) = (1 - 3) / (1 - 0)

m = -2/1

m = -2

Equation of the falling line :

y = -2x + 3

By applying one of the points from the solution region in option D, we get

So, option D is correct.

Problem 3 :

If the system of inequaliites y ≥ 2x + 1 and y > (1/2)x - 1 is graphed in the xy-plane above, which quadrant contains no solution to the system ?

a) Quadrant II      b)  Quadrant III      c)  Quadrant IV

d) There are solutions in all four quadrants

Solution :

Solving the system of inequalities given,

y ≥ 2x + 1 and y > (1/2)x - 1

To determine which quadrant does not contain any solutions to the system of inequalities, graph the inequalities. Graph the inequality y ≥ 2x + 1 by drawing a line through the y-intercept (0,1) and the point (1,3), and graph the inequality y > (1/2)x - 1 by drawing a dashed line through the y-intercept (0,−1) and the point (2,0), as shown in the figure below.

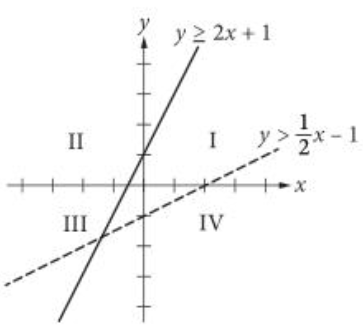
The solution to the system of inequalities is the intersection of the shaded regions above the graphs of both lines. It can be seen that the solutions only include points in quadrants I, II, and III and do not include any points in quadrant IV.

Choices A and B are incorrect because quadrants II and III contain solutions to the system of inequalities, as shown in the figure above. Choice D is incorrect because there are no solutions in quadrant IV.

Problem 4 :

y ≤ x + 7

y ≥ -2x - 1

Which point (x, y) is the solution to the given system of inequalities in the xy plane.

a)  (-14, 0)     b)  (0, -14)     c)  (0, 14)     d)  (14, 0)

Solution :

So, option d is correct.