WRITING INEQUALITIES FOR THE UNSHADED REGION SHOWN IN THE GIVEN FIGURE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Equation of horizontal lines will be in the form,
y = a or y = -a
Equation of vertical lines will be in the form,
x = a or x = -a
Equation of slanting line will be in the form
a x + by = c
The following inequalities can be used,
|
< > ≤ ≥ |
Less than Greater than Less than or equal to Greater than or equal to |
- We have to use < or > sign when we have dotted line.
- We have to use ≤ or ≥ sign, when we have solid line.
Write the inequalities to represent the following unshaded regions :
Problem 1 :
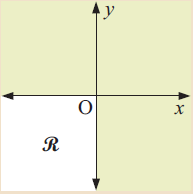
Solution :
The unshaded region is the third quadrant. All the values of x is lesser than 0 and values of y are less than 0. Then,
x ≤ 0 and y ≤ 0
Problem 2 :
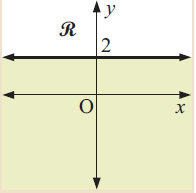
Solution :
The given line is the horizontal line, it will be in the form y = a. The horizontal line passes through 2. Writing it as linear function, y = 2.
By considering the unshaded region, the values are greater than 2. So, the inequality representing the unshaded region is
y ≥ 2
Problem 3 :
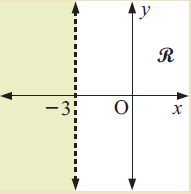
Solution :
The given line is the vertical line, it will be in the form x = a. The horizontal line passes through -3. Writing it as linear function, x = -3.
By considering the unshaded region, the values are lesser than -3. So, the inequality representing the unshaded region is
x > -3
Problem 4 :
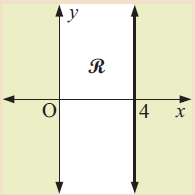
Solution :
The shown lines are vertical lines. Both are solid lines. Then we can use ≤ or ≥ signs based on the unshaded region. writing as linear functions, we get
x = 4 and x = 0
To the right of x = 0, the unshaded region is greater than 0. Considering to the left of 4, all the values are lesser than 4. Then inequality representing the unshaded region is
x ≥ 0 and x ≤ 4
Problem 5 :
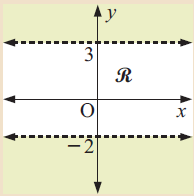
Solution :
The shown lines are horizontal lines. Both are dotted lines. Then we can use < or > signs. By writing linear functions, we get
y = -2 and y = 3
Now by considering the unshaded region,
- all the values above y = -2 are greater than -2.
- all the values below y = 3 are lesser than 3.
Representing as inequalities, we get
y > -2 and y < 3
(or)
-2 < y < 3
Problem 6 :
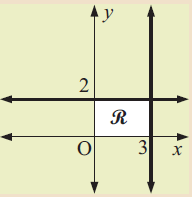
Solution :
In the lines shown above, one line is horizontal line and another is a vertical line. Writing the linear function, we get
- Equation of horizontal line is y = 2
- Equation of vertical line is x = 3
Considering the unshaded region, all the y values below y = 2 are smaller than 2.
All the x values towards left of 3 are lesser than 3.
Representing as inequalities, we get
0 ≤ y ≤ 2 and 0 ≤ x ≤ 3
Problem 7 :
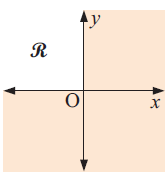
Solution :
The unshaded region is in the first quadrant. Considering the linear function x = 0, the values of y are greater than 0.
Considering the linear function y = 0, the values of x are lesser than 0.
Converting the linear function as inequalities, we get.
y ≥ 0 and x ≤ 0
Problem 8 :
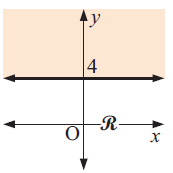
Solution :
The given line is a solid line and it is horizontal line, Considering the linear function y = 4, all the y - values below the linear function or unshaded the region are lesser than 4.
Converting the linear function as inequalities, we get.
y ≤ 4
Problem 9 :
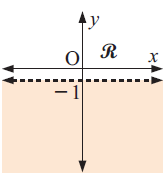
Solution :
The given line is a dotted line and it is horizontal line, Considering the linear function y = -1, all the y - values below the linear function or unshaded the region are greater than -1.
Converting the linear function as inequalities, we get.
y > -1
Problem 10 :
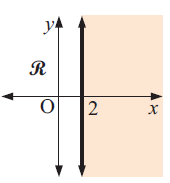
Solution :
The given line is a solid line and it is vertical line, Considering the linear function x = 2, all the y - values below the linear function or unshaded the region are lesser than 2
Converting the linear function as inequalities, we get.
x < 2
Problem 11 :
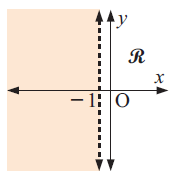
Solution :
The given line is a dotted line, considering the linear function x = -1, all the x - values to the right of -1 are greater than -1.
Converting the linear function as inequalities, we get.
x > -1
Problem 12 :
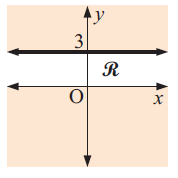
Solution :
The shaded region is below x = 3 and above x = 0. We have solid lines. Converting the linear function as inequalities, we get.
y < 3 and y > 0
Problem 13 :
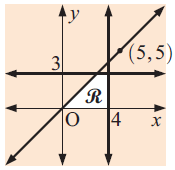
Solution :
Finding the equation of slanting line :
Two points on the slanting line are (0, 0) and (5, 5)
Slope (m) = (y2 - y1) / (x2 - x1)
m = (5 - 0) / (5 - 0)
m = 1 and y-intercept (b) = 0
y = mx + b
y = 1x + 0
Linear function representing the slanting line is y = x
Linear inequality function is y ≤ x
- Equation of horizontal line is y = 3
- Equation of vertical line is x = 4.
Considering the unshaded region, by converting into linear inequality, we get
y ≤ 3 and x ≤ 4
So, the unshaded region represented by the figure is
y ≤ x, y ≤ 3 and x ≤ 4.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling