WRITE THE VERBAL MEANING FOR INEQUALITY STATEMENT

Problem 1 :

{x : x > 4}

Solution :

How to define the values of x ?

From x > 4, we understand that all values which are greater than 4. Here 4 should not be included.

Problem 2 :

{x : x ≤ 5}

Solution :

How to define the values of x ?

From x ≤ 5, we understand that all values of x are lesser than or equal to 5. Here 5 should be included.

Problem 3 :

{y : 0 < y < 8}

Solution :

How to define the values of y ?

From y < 8, we understand that all  values of y lies in between 0 and 8. Here 0 and 8 are not be included.

Problem 4 :

{y : 1 ≤ y ≤ 4}

Solution :

How to define the values of y ?

From 1 ≤ y ≤ 4, we understand that all values of y lies in between 0 and 4. Here 0 and 4 both should be included.

Problem 5 :

{t : 2 < t < 7}

Solution :

How to define the values of t ?

From 2 < t < 7, we understand that all values of t lies in between 2 and 7. Here 2 and 7 both should not be included.

Problem 6 :

{n : n ≤ 3 or n > 6}

Solution :

How to define the values of n ?

Considering n ≤ 3, all values of n are lesser than or equal to 3. Here 3 should also be included.

Considering n > 6, all the values of n are greater than 6. Notice that 6 should not be included.

Problem 7 :

{x : 4 ≤ x < 8}

Solution :

How to define the values of x ?

From 4 ≤ x < 8, we understand that all the values of x lies in between 4 and 8. Here 4 should be included and 8 should not be included.

Problem 8 :

{x : -5 < x ≤ 4}

Solution :

How to define the values of x ?

From -5 < x ≤ 4, we understand that all the values of x lies in between -5 and 4. Here -5 should not be included and 4 should be included.

Problem 9 :

{x : -5 ≤ x ≤ 0}

Solution :

How to define the values of x ?

From -5 ≤ x ≤ 0, we understand that all the values of x lies in between -5 and 0. Here -5 and 0 are to be included.

Problem 10 :

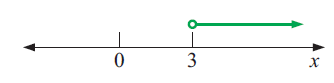
Solution :

By observing the number line shown above, the solution is to the right of 3. Since we have transparent circle or open circle near 3, we should not include this 3.

Possible values of x are greater than 3.

Problem 11 :

Solution :

By observing the number line shown above, the solution lies in between 2 and 5. Near 2, we have transparent circle and near 5 we have solid circle.

So, the possible values of x are greater than 2 and lesser than or equal to 5.

Problem 12 :

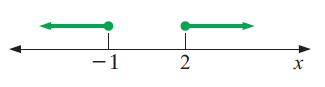
Solution :

By observing the number line shown above, the solution are 

to the left of -1 and to the right of 2

Near both values, we have solid circle. So, these two values to be included in the solution.

Then, the possible values of x are lesser than or equal to -1 and greater than or equal to 2.

Problem 13 :

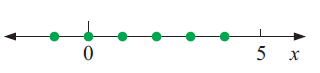
Solution :

By observing the number line shown above, the solution are some selected values. Particularly integers are solutions.

So, possible values of x are -1, 0, 1, 2, 3, 4. 

Verbal meaning :

The solutions are integers which is greater than -1 and less than 5 only integers.

Problem 14 :

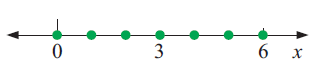
Solution :

By observing the number line shown above, the solution are some selected values. Particularly integers are solutions.

So, possible values of x are 0, 1, 2, 3, 4, 5, 6

Verbal meaning :

The solutions are integers which is greater than or equal to 0 and lesser than or equal to 6.

Problem 15 :

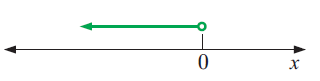
Solution :

By observing the number line shown above, the solution lies to the left of 0. So, the possible values of x are less than 0.