WRITE THE PRIME FACTORIZATION OF THE NUMBER

Write the prime factorization of the number:

Problem 1 :

26

Solution :

Decompose 26 into prime factors using division method.

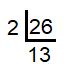Problem 2 :

58

Solution :

Decompose 58 into prime factors.

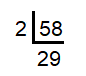Problem 3 :

63

Solution :

Decompose 63 into prime factors.

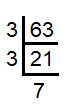Problem 4 :

85

Solution :

Decompose 85 into prime factors.

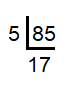Problem 5 :

120

Solution :

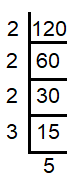
Decompose 120 into prime factors.

Problem 6 :

160

Solution :

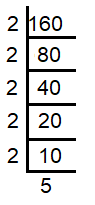
Decompose 160 into prime factors.

Problem 7 :

154

Solution :

Decompose 154 into prime factors.

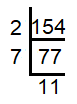Problem 8 :

195

Solution :

Decompose 195 into prime factors.

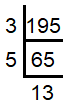Problem 9 :

225

Solution :

Decompose 225 into prime factors.

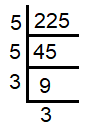Problem 10 :

210

Solution :

Decompose 210 into prime factors.

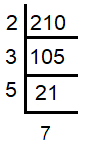Problem 11 :

What is the greatest perfect square that is a factor of 1575?

Solution :

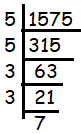
The prime factorization shows that 1575 has three factors other than 1 that are perfect squares.

3 ⋅ 3 = 9

5 ⋅ 5 = 25

(3 ⋅ 5) ⋅ (3 ⋅ 5) = 15 ⋅ 15 = 225

So, the greatest perfect square that is a factor of 1575 is 225.

Problem 12 :

What is the greatest perfect square that is a factor of 396? Explain.

Solution :

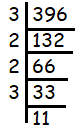
396 = 3 x 2 x 2 x 3 x 11

Grouping into pairs, we get

= 3 x 3 x 2 x 2 x 11

(3 x 3) x (2 x 2) = 9 x 4

= 36

So, the greatest perfect square in 396 is 36.

Problem 13 :

Describe and correct the error in writing the prime factorization.

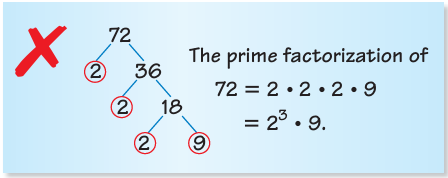
Solution :

Here prime factorization is not completed. 9 is composite number.

9 = 3 x 3

72 = 2 x 2 x 2 x 3 x 3

Problem 14 :

Find the number represented by the prime factorization.

a)  2² ⋅ 3² ⋅ 5

b)  3² ⋅ 5² ⋅ 7

c)  2³ ⋅ 11² ⋅ 13

Solution :

a)  2² ⋅ 3² ⋅ 5

= 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 5

= 4 ⋅ 9 ⋅ 5

= 180

b)  3² ⋅ 5² ⋅ 7

= 3 ⋅ 3 ⋅ 5 ⋅ 5 ⋅ 7

= 9 ⋅ 25 ⋅ 7

= 1575

c)  2³ ⋅ 11² ⋅ 13

= 2 ⋅ 2 ⋅ 2 ⋅ 11 ⋅ 11 ⋅ 13

= 8 ⋅ 121 ⋅ 13

= 12584

Problem 15 :

Find the greatest perfect square that is a factor of the number.

a)  244

b)  650

c)  756

d)  1290

Solution :

a)

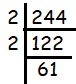
Prime factorization of 244 = 2 x 2 x 61

The perfect square is 2 x 2, which is 4. So, greatest perfect square in 244 is 4.

b)

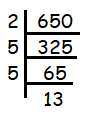
Prime factroization of 650 = 2 x 5 x 5 x 13

The pefect square is 5 x 5, which is 25. So, the greatest perfect square in 650 is 25.

c) 

Prime factorization of 756 = 2 x 2 x 3 x 3 x 3 x 7

The perfect square = 2 x 2 x 3 x 3

= 4 x 9

= 36

So, the greatest perfect square in 756 is 36.

d)

Prime factorization of 1290 = 2 x 5 x 3 x 43

We dont find any pairs, so there is no pefect square.

Problem 15 :

The coach of a baseball team separates the players into groups for drills. Each group has the same number of players. Is the total number of players on the baseball team prime or composite? Explain

Solution :

By understanding the given situation, we know that each group as same number of players.

To find total number of players, we have to add the number of players in each group.

Case 1 : (Prime and prime)

For example, let us consider there are 2 members in each group and there are 5 groups. To find total number of members, we should multiply 2 by 5 and we get 10. Finally we get composite number.

Case 2 : (Prime and composite)

For example, let us consider there are 3 members in each group and there are 10 groups. To find the total number of members, we should multiply 3 by 10 and we get 30. Finally we get the composite number.

or