WRITE THE FRACTION REPRESENTING THE SHADED PORTION

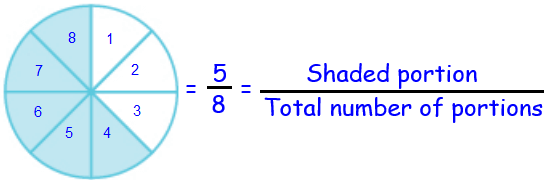
Name the fraction of each figure that is shaded 

Problem 1 :

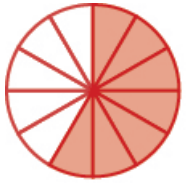
Solution :

Total portions = 12

Shaded portions = 7

Fraction form = 7/12

Problem 2 :

Solution :

Total portions = 9

Shaded portions = 4

Fraction form = 4/9

Problem 3 :

Solution :

Total portions = 4

Shaded portions = 3

Fraction form = 3/4

Problem 4 :

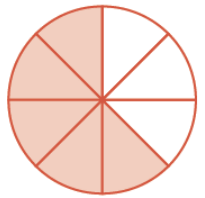
Solution :

Total portions = 8

Shaded portions = 5

Fraction form = 5/8

Problem 5 :

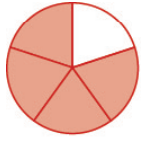
Solution :

Total portions = 5

Shaded portions = 4

Fraction form = 4/5

Problem 6 :

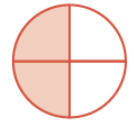
Solution :

Total portions = 4

Shaded portions = 2

Fraction form = 2/4

Problem 7 :

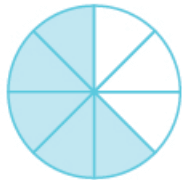
Solution :

Total portions = 8

Shaded portions = 5

Fraction form = 5/8

Problem 8 :

Solution :

Total portions = 9

Shaded portions = 5

Fraction form = 5/9

Problem 9 :

Solution :

Total portions = 8

Shaded portions = 3

Fraction form = 3/8

Problem 10 :

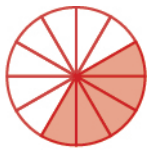
Solution :

Total portions = 12

Shaded portions = 5

Fraction form = 5/12

Write the shaded part of the unit square as a decimal. Then write the decimal as a fraction.

Problem 11 :

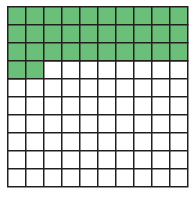
Solution :

Total number of squares = 100

Number of shaded squarees = 30 + 2

= 32

Representing it as fraction = 32/100

Converting into decimal,

= 0.32

Problem 12 :

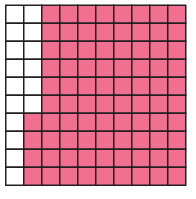
Solution :

Total number of squares = 100

Number of shaded squarees = 80 + 4

= 84

Representing it as fraction = 84/100

Converting into decimal,

= 0.84

Problem 13 :

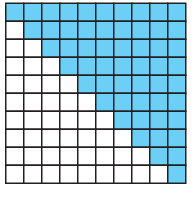
Solution :

Total number of squares = 100

Considering from left to right, number of squares which are shaded 

= 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1

Sum of n natural numbers = n(n + 1) / 2

= (10 x 11) / 2

= 55

Number of shaded squarees = 55

Representing it as fraction = 55/100

Converting into decimal,

= 0.55

The area model represents the multiplication of two fractions. Copy and complete the statement

Problem 14 :

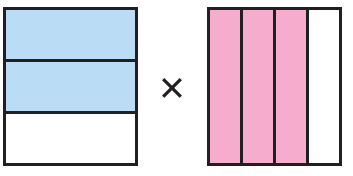
Solution :

Fraction represented by the first = 2/3

Fraction represented by the second = 3/4

Multiplying these two fractions, we get

= 2/3 x 3/4

= (2 x 3) / (3 x 4)

= 6/12

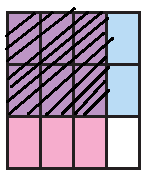
Shading 6 sparts out of 12.

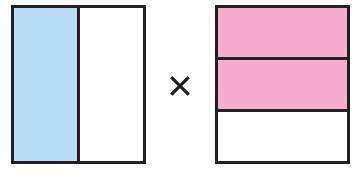
Problem 15 :

Solution :

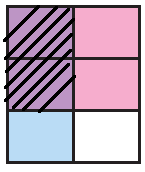
Fraction represented by the first = 1/2

Fraction represented by the second = 2/3

Multiplying these two fractions, we get

= 1/2 x 2/3

= (1 x 2) / (2 x 3)

= 2/6

Problem 16 :

Solution :

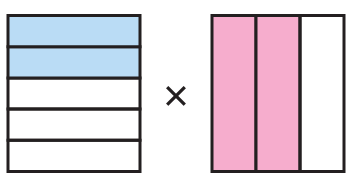
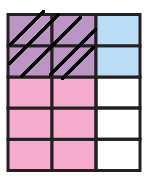
Fraction represented by the first = 2/5

Fraction represented by the second = 2/3

Multiplying these two fractions, we get

= 2/5 x 2/3

= (2 x 2) / (5 x 3)

= 4/15

Problem 17 :

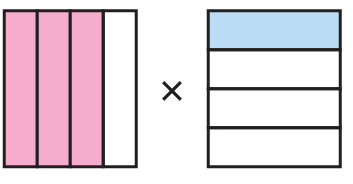
Solution :

Fraction represented by the first = 3/4

Fraction represented by the second = 1/4

Multiplying these two fractions, we get

= 3/4 x 1/4

= (3 x 1) / (4 x 4)

= 3/16

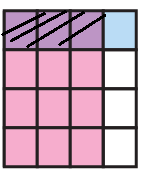
Problem 18 :

What is the missing denominator?

3/7 × 1/? = 3/28

Solution :

3/7 × 1/? = 3/28

To multiply two fractions, first we have to multiply the numerator by the numerator, denominator by the denominator.

(3 x 1) / (7 x ?) = 3/28

7 should be multiplied by 4, then we will get 28.

So, the missing number is 4.

Problem 19 :

You make a banner for a football rally.

a. What is the area of the banner?

b. You add a 1/4 -foot border on each side. What is the area of the new banner?

Solution :

a)

Length = 4   2/3 ft

width = 1  1/2 ft

Area of banner = lenght x width

= 4  2/3  x 1  1/2

= 14/3 x 3/2

= 7 square feet

b)

After adding 1/4 foot is added,

the new length = 14/3 + 1/4 + 1/4

= 14/3 + 2/4

= (56 + 6)/12

= 62/12 ==> 31/6

New width = 3/2 + 1/4 + 1/4

= (6 + 1 + 1)/4

= 8/4

= 2

New area = 31/6 x 2

= 31/3 square feet

= 10.3 square feet

Problem 20 :

A bottle of juice is 2/3 full. The bottle contains 4/5 of a cup of juice.

a. Write a division expression that represents the capacity of the bottle.

b. Write a related multiplication expression that represents the capacity of the bottle.

c. Explain how you can use the diagram to verify the expression in part (b).

d. Find the capacity of the bottle.

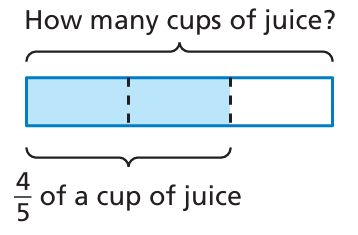
Quantity of juice in bottle = 2/3 of capacity of bottle

or 4/5 of cup of juice

a)  Capacity of bottle = 4/5 ÷ 2/3

b)  Multiplication expression = 4/5 x 3/2

c)  Multiplying the numerator by numerator, denominator by denominator we get

= (4 x 3)/(5 x 2)

= 12/10

= 6/5

d) Capacity of bottle is 6/5 cups.