WRITE EQUATIONS FOR PROPORTIONAL RELATIONSHIPS WORD PROBLEM WORKSHEET

Problem 1 :

John and Amber work at an ice cream shop. The hours worked and wages earned are given for each person.

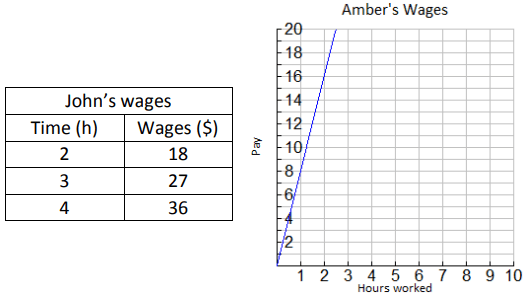
a) Are John’s wages proportional to time. How do you know? If they are, determine the unit rate.

b) Are Amber’s wages proportional to time. How do you know? If they are, determine the unit rate.

c) Write an equation to model the relationship between each person’s wages. Identify the constant of proportionality for each.

d) How much would each worker make after working 10 hours? Who will earn more money?

Solution

Problem 2 :

It cost $5 to send 6 packages through a certain shipping company. Consider the number of packages per dollar.

a)  Find the constant of proportionality for this situation.

b)  Write an equation to represent the relationship.

Solution

Problem 3 :

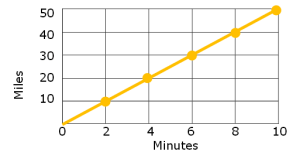
Write an equation that will model the proportional relationships shown in the graph below graph.

Solution

Problem 4 :

Jennifer is shopping with her mother. They pay $2 per pound for tomatoes at the vegetable stand.

a) Write an equation to represent the proportional relationship.

b) How much will Jennifer pay if she buys 5.3 pounds of tomatoes?

Solution

Problem 5 :

In Katya's car, the number of miles driven is proportional to the number of gallons of gas used. Find the missing value in the table.

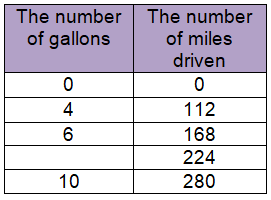
a) Write an equation that will relate the number of miles driven  to the number of gallons of gas.

b) What is the constant of proportionality ?

c) How many miles could Katya go if she filled her 22 gallon tank ?

d)  If Katya takes a trip of 600 miles, how many gallons of gas would be needed to make the trip ?

e) If Katya drives 224 miles during one week of commuting to school and work, how many gallons of gas would she use ?

Solution