WRITE AND GRAPH A DIRECT VARIATION EQUATION WITH THE POINT

Problem 1 :

Write and graph a direct variation equation that has a solution (3, -9).

Solution :

Direct variation equation passing through the point (3, -9)

When x = 3, y = -9

Direct variation equation y = ax

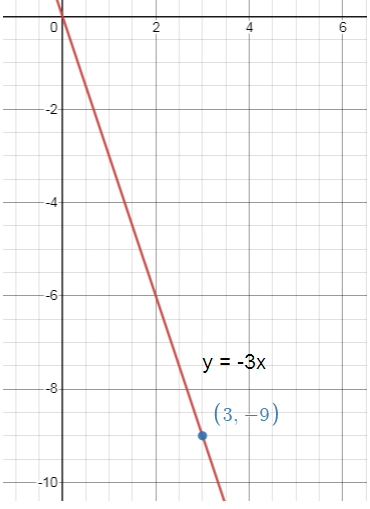
Problem 2 :

Write and graph a direct variation equation that has a solution (-7, 4).

Solution :

Direct variation equation passing through the point (-7, 4)

x = -7, y = 4

Direct variation equation y = ax

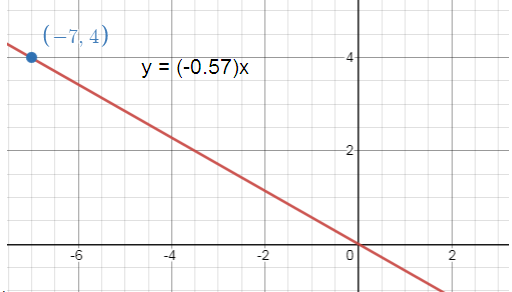
Problem 3 :

Write and graph a direct variation equation that has a solution (5, 3).

Solution :

Direct variation equation passing through the point (5, 3).

x = 5, y = 3

Direct variation equation y = ax

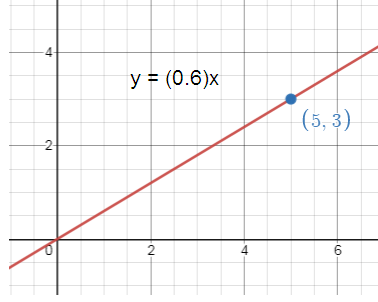
Problem 4 :

Write and graph a direct variation equation that has a solution (6, -2).

Solution :

Direct variation equation passing through the point (6, -2).

x = 6, y = -2

Direct variation equation y = ax

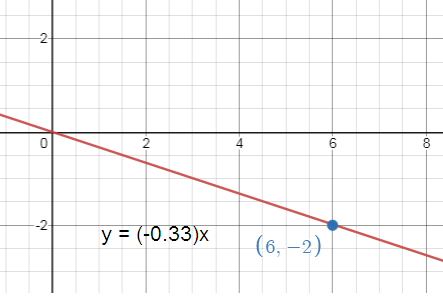
Problem 5 :

A charter bus travels 210 miles in 3 1/2 hours. Assume the distance traveled varies directly with time traveled. Write and solve a direct variation equation to find how far the bus will travel in 6 hours.

Solution :

Let D be the distance traveled and t be the time taken.

D ∝ t

D = kt

When D = 210 miles, t = 3.5 hours

210 = k(3.5)

k = 210/3.5

k = 60

Applying the value of k, we get

D = 60t

When t = 6, we get

D = 60(6)

= 360 miles

So, in 6 hours the distance traveled is 360 miles.

Problem 6 :

The cost of papers varies directly with the number of reams bought. Suppose two reams cost $5.10. Write a direct variation equation to represent this relationship. Then identify the constant of variation and interpret its meaning.

Solution :

1 ream = 500 sheets

2 reams = 1000 sheets

Let C be the cost and R be the reams

C ∝ R

C = kR

5.10 = k(2)

k = 5.10/2

k = 2.55

C = 2.55R

Problem 7 :

The amount of flour needed for a recipe varies directly with the number of servings planned. Three servings required 4 1/2 cups of flour. Write the direct variation equation to represent this relationship. Then identify the constant of variation and interpret its meaning.

Solution :

Let F be the quantity of flour needed as cups and number of servings be N.

N ∝ F

N = kF

3 = k(4.5)

k = 3/4.5

k = 0.66

By applying the value of k, we get

N = 0.66 F

Problem 8 :

The cost of apps varies directly with the number of apps purchases. Aditi bought four apps for total of $5.16. She found the direct variation equation below for this relationship. Find her mistake and correct it.

y = 5.16x

Solution :

y be the cost of apps and x be the number of apps.

y ∝ x

y = kx

5.16 = k(4)

k = 5.16/4

k = 1.29

y = 1.29x

In the given equation, it is given that the constant of variation is 5.16 and that is the error.

Problem 9 :

Water pressure is measured in pounds per square inch (psl). The number of pounds per square inch y varies directly with the depth x of the water. Write and solve a direct variation equation to determine what the pressure is at a depth of 297 feet.

Solution :

y ∝ x

y = kx

29 = k(66)

k = 29/66

y = (29/66)x

When depth = 297 feet

y = (29/66)(297)

y = 130.5