WRITE AN EQUATION OF THE LINE WITH THE GIVEN SLOPE AND Y-INTERCEPT

Write down the equation of a line with :

Problem 1:

Gradient 2 and y-intercept 11

Solution :

Write the slope - intercept form equation of a line:

y = mx + b

Substitute 2 for m and 11 for b

y = 2x + 11

2x - y + 11 = 0

Hence, the equation of a line is 2x - y + 11 = 0.

Problem 2 :

Gradient 4 and y-intercept -6

Solution :

Write the slope - intercept form equation of a line:

y = mx + b

Substitute 4 for m and -6 for b

y = 4x - 6

4x - y - 6 = 0

Hence, the equation of a line is 4x - y - 6 = 0.

Problem 3 :

Gradient -3 and y-intercept 1/2

Solution :

Write the slope - intercept form equation of a line:

y = mx + b

Substitute -3 for m and 1/2 for b

y = -3x + 1/2

3x + y - 1/2 = 0

6x + 2y - 1 = 0

Hence, the equation of a line is 6x + 2y - 1 = 0.

Problem 4 :

Gradient -1 and y-intercept 4

Solution :

Write the slope - intercept form equation of a line:

y = mx + b

Substitute -1 for m and 4 for b

y = -x + 4

x + y - 4 = 0

Hence, the equation of a line is x + y - 4 = 0.

Problem 5 :

Gradient 0 and y-intercept 7

Solution :

Write the slope - intercept form equation of a line:

y = mx + b

Substitute 0 for m and 7 for b

y = 0 + 7

 y - 7 = 0

Hence, the equation of a line is y - 7 = 0.

Problem 6 :

Gradient 2/3 and y-intercept 6

Solution :

Write the slope - intercept form equation of a line:

y = mx + b

Substitute 2/3 for m and 6 for b

y = (2/3)x + 6

(2/3)x - y + 6 = 0

2x - 3y + 18 = 0

Hence, the equation of a line is 2x - 3y + 18 = 0. 

Problem 7 :

You have $110 in your lunch account and plan to spend $2.75 each school day.

a. Write and graph a linear equation that represents the balance in your lunch account.

b. How many school days will it take to spend all of the money in your lunch account?

Solution :

Amount i have = $110

Amount i spend on each day = $2.75

Let x be the number of days. Let y be amount you have in your account.

a) y = 110 - 2.75x

Finding x and y-intercepts :

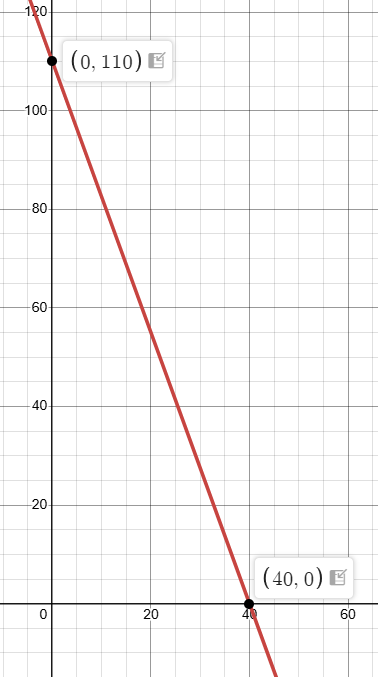
b) It will take 40 days to spend all the money.

Problem 8 :

The equation 22 = 2y + x represents the perimeter of a flower garden with length y (in feet) and width x (in feet). Solve for y. Then find the length of the flower garden when the width is 2 feet, 3 feet, and 4 feet

Solution :

22 = 2y + x

x - width and y - length

2y = -x + 22

y = (-1/2)x + (22/2)

y = (-1/2)x + 11

• When width is 2 feet, then length is 10 feet
• When width is 3 feet, then length is 19/2 feet
• When width is 4 feet, then length is 9 feet

Problem 9 :

The equation 0.60 = 0.05x + 0.10y represents the number of nickels x and dimes y needed to add up to 60 cents. Solve for y. Then find the number of dimes that are needed to make 60 cents when the number of nickels is 0, 2, and 4.

Solution :

0.60 = 0.05x + 0.10y

x - nickels y - dimes

0.10y = -0.05x + 0.60

y = -0.05x/0.10 + 0.60/0.10

y = -0.5x + 6

• When 0 nickels number of dimes will be 6
• When 2 nickels number of dimes will be 5
• When 4 nickels number of dimes will be 4

Problem 10 :

The distance your friend travels y (in miles) running x hours is represented by the equation y = 7.5x.

a. Graph the equation and interpret the slope.

b. How many minutes does it take for your friend to run one mile?

Solution :

a) y = 7.5x

The slope of 7.5 represents your friend's constant running speed of 7.5 miles per hour. For every one hour your friend runs, they cover a distance of 7.5 mile

b) 7.5 miles per hour. Converting into minutes, we get

= 60/7.5

= 8 minutes