WRITE AN EQUATION OF A PARABOLA WITH THE GIVEN VERTEX AND FOCUS

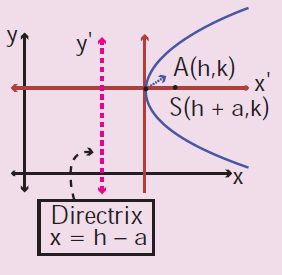
Equation of parabola which is symmetric about x-axis and open rightward.

(y - k)² = 4a(x - h)

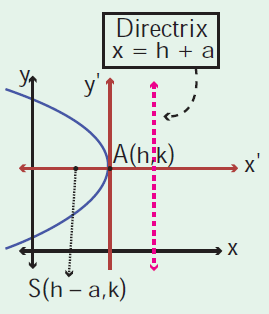
Equation of parabola which is symmetric about x-axis and open leftward.

(y - k)² = -4a(x - h)

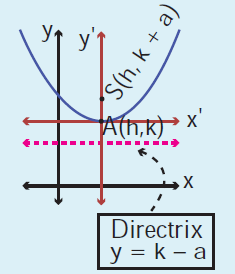
Equation of parabola which is symmetric about y-axis and open upward.

(x - h)² = 4a(y - k)

 Equation of parabola which is symmetric about y-axis and open downward.

(x - h)² = -4a(y - k)

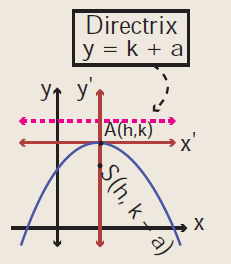
Write an equation for each parabola described below. Then draw the graph.

Problem 1 :

Vertex (0, 1) and focus (0, 5)

Solution :

The parabola is symmetric about y-axis and it opens up.

(x - h)² = 4a(y - k)

Applying vertex (0, 1), we get

(x - 0)² = 4a(y - 1)

x² = 4a(y - 1)  -----(1)

Distance between vertex and focus = a

= √(x₂ - x₁)² + (y₂ - y₁)²

Vertex (0, 1) and focus (0, 5)

= √(0 - 0)² + (5 - 1)²

a = 4

Applying the value of a in (1), we get

x² = 4(4)(y - 1) 

x² = 16(y - 1) 

x² = 16y - 16

16y = x² + 16

y = (1/16) x² + 1

Problem 2 :

Vertex (8, 6) and focus (2, 6)

Solution :

The parabola is symmetric about x-axis and it opens rightward. By drawing the figure with the given information, we come to know that

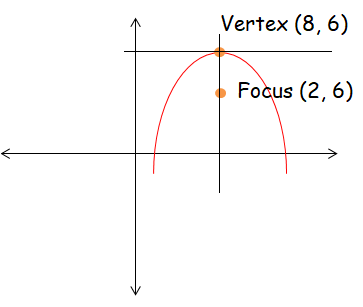
(y - k)² = -4a(x - h)

Applying vertex (8, 6), we get

(y - 6)² = -4a(x - 8)  -----(1)

Distance between vertex and focus = a

= √(x₂ - x₁)² + (y₂ - y₁)²

Vertex (8, 6) and focus (2, 6)

= √(2 - 8)² + (6 - 6)²

= √(-6)² + 0²

a = 6

Applying the value of a in (1), we get

(y - 6)² = -4(6)(x - 8)

(y - 6)² = -24(x - 8)

x - 8 = (-1/24)(y - 6)²

x = (-1/24)(y - 6)² + 8

Problem 3 :

Vertex (5, -1) and focus (3, -1)

Solution :

The parabola is symmetric about x-axis.

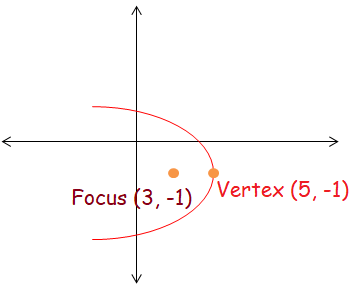
Solution :

The parabola is symmetric about x-axis and it opens leftward. By drawing the figure with the given information, we come to know that

(y - k)² = -4a(x - h)

Applying vertex (5, -1), we get

(y - (-1))² = -4a(x - 5)

(y + 1)² = -4a(x - 5)  -----(1)

Distance between vertex and focus = a

= √(x₂ - x₁)² + (y₂ - y₁)²

Vertex (5, -1) and focus (3, -1)

= √(3 - 5)² + (-1 + 1)²

= √(-2)² + 0²

a = 2

Applying the value of a in (1), we get

(y + 1)² = -4(2)(x - 5)

(y + 1)² = -8(x - 5)

(-1/8) (y + 1)² = x - 5

x = (-1/8) (y + 1)² + 5

Problem 4 :

When a ball is thrown or kicked, the path it travels is shaped like a parabola. Suppose a football is kicked from ground level, reaches a maximum height of 25 feet, and hits the ground 100 feet from where it was kicked. Assuming that the ball was kicked at the origin, write an equation of the parabola that models the flight of the ball.

Solution :

From the given information, the parabola is open downward.

The maximum height = 25

Maximum point will be at vertex, then k = 25

When it reaches the ground, the horizontal distance covered is 100 feet.

To find out h, we can find the mid point of the horizontal distance covered by the ball.

h = 100/2 ==> 50

Vertex is at (50, 25)

One of the points on the parabola is (100, 0)

(x - h)² = -4a(y - k)

(x - 50)² = -4a(y - 25) ------(1)

Applying the point (100, 0) here, we get

(100 - 50)² = -4a(0 - 25)

(50)² = 100a

a = 2500/100

a = 25

Applying the value of a in (1), we get

(x - 50)² = -4(25)(y - 25) 

(x - 50)² = -100(y - 25) 

y - 25 = (-1/100) (x - 50)²

y = (-1/100) (x - 50)² + 25

Problem 5 :

A microphone is placed at the focus of a parabolic reflector to collect sound for the television broadcast of the world cup soccer game. Write an equation for the cross section, assuming that the focus is at the origin and the parabola opens to the right.

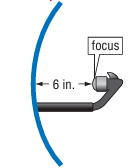
Solution :

Since the parabola opens right, equation of parabola will be

(y - k)² = 4a(x - h)

Here focus is at origin.  Vertex will be at (-6, 0)

(y - 0)² = 4a(x + 6)

Distance between vertex focus = a

a = 6

y² = 4(6)(x + 6)

y² = 24(x + 6)

x + 6 = (1/24)y²

x = (1/24)y² - 6