WRITE A LINEAR MODEL FROM WORD PROBLEM WORKSHEET

1)  The function below shows the cost of a hamburger with different numbers of toppings (t).

f(t) = 1.90 + 1.40t

a) What is the y-intercept, and what does it mean?

b) What is the slope, and what does it mean?

c) If Jodi paid $3.30 for a hamburger, how many toppings were on Jodi’s hamburger?

Solution

2)  The function below shows the cost of an ice cream sundae with different numbers of toppings (t).

f(t) = 2.25 + 0.75t

a) What is the y-intercept, and what does it mean?

b) What is the slope, and what does it mean?

Solution

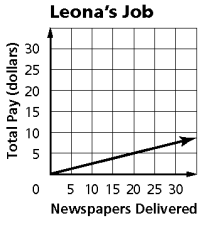
3)  The graph below shows the number of newspapers delivered and total pay for Leona’ newspaper delivery job. What does the slope ? 

Solution

4)  Dionne pays a fixed fee plus an hourly rate to rent a boat. The table below shows how much Dionne paid for the boat. What was Dionne’s hourly rate to rent the boat?

Solution

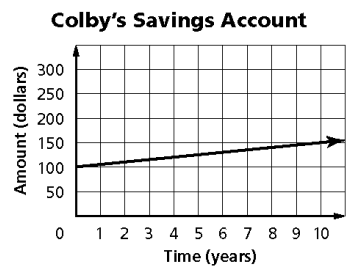
5)  Colby put $100 in a savings account. The graph below shows  how the amount in the account would increase over the next ten years. What does the y-intercept represent? 

Solution

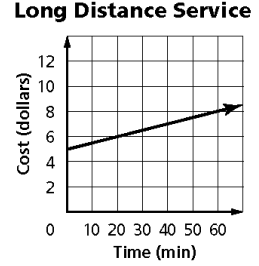
6)  Tara pays a base rate for her long distance phone service plus a per-minute charge. The graph below shows what she would pay for her long distance phone service for the first 60 minutes. What does the y-intercept of this graph represent? 

Solution

7)  Rich is a member of a gym. He pays a monthly fee plus a per-visit fee. The equation below represents the monthly amount Rich pays for his membership to the gym per month for x visits.

y = 3x + 10

What does the y-intercept of the graph of this equation represent?             Solution

Write an equation, in slope-intercept form, to model each situation.

Problem 1 :

You rent a bicycle for $20 plus $2 per hour.

Solution

Problem 2 :

In 1995, Orlando, Florida, was about 175,000. At that time, the population was growing at a rate of about 2000 per year. Write an equation, in slope-intercept form to find Orlando’s population for any year

a) Predict what Orlando’s population will be in 2010

Solution

Problem 3 :

Couples are marrying later. The median age of men who tied the knot for the first time in 1970 was 23.2. In 1998, the median age was 26.7. Write an equation, in slope intercept form to predict the median age that men marry M for any year t.

Use the to predict the median age of men who marry for the first time in 2005.

Solution

Problem 4 :

Carmela is a member of a social club. She pays an annual membership fee and $15 for each event she attends. The equation y = 15x + 25 represents her total cost each year. Which statement(s) about the function is true?

(Hint: three of these are true)

A. The initial value is 15.

B. x represents the cost of each event.

C. The rate of change is 15.

D. The initial value represents the annual membership fee.

E. The number of events she attends is a function of the total cost.

F. The total cost is a function of the number of events she attends.

Solution

Problem 5 :

Vinh pays a convenience fee when he reserves movie ticket son his cell phone app. The app shows him the total cost of his purchase for different number of tickets in the table shown.

a) What is the equation that models this linear function? Show your work.

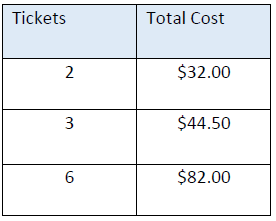
b) How much is each movie ticket?              Solution

Problem 6 :

You and your friend are riding bicycles down the same road at different constant speeds. After 3 minutes, you are 60 feet ahead of your friend. After 5 minutes, you are 100 feet ahead of your friend.

a. Write an equation that represents the distance y (in feet) you are ahead of your friend after x minutes.

b. How far ahead will you be after 10 minutes?

Solution

Problem 7 :

You are knitting a blanket at a rate of 4 inches per day. After 4 days, you have knitted 16 inches.

a. Write an equation that represents the number of inches y you have knitted after x days.

b. How many inches will you have knitted after 7 days?

c. Will you have knitted 100 inches after 30 days?

Solution