WRITE A LINEAR INEQUALITY OF TWO VARAIBLES FROM A GRAPH

Problem 1 :

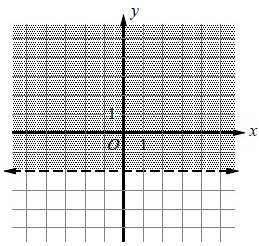
Which of the following inequalities represents the graph above?

a. x > -2      b. x < -2      c. y > -2       d. y < -2

Solution :

By observing the graph, the dotted line passes through y = -2. Comparing with other values on y-axis, -1, 0, 1,...... are greater than -2.

So,

y > -2

Problem 2 :

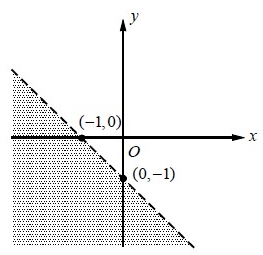
Which of the following inequalities represents the graph above?

a. x + y < -1           b. x + y > -1

c. x + y ≤ - 1          d. x + y ≥ -1

Solution :

Rise = -1 and Run = 1

Slope = -1/1 = -1

y- Intercept = -1

So, the equation of the given line is

y = -x - 1

Take the point (-2, -2) and apply it in the equation

y = -x - 1

-2 = 2 - 1

-2 = 1

Here -2 is less than 1, so we have to choose the < instead of equal sign in the equation y = -x - 1.

y < - x - 1

x + y  < -1

Hence, the required inequality is

x + y < -1

Problem 3 :

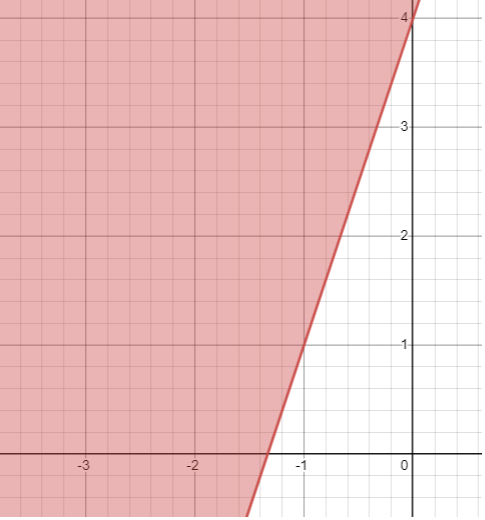
Solution :

y- Intercept = 4

Slope :

Rise = down 3 units ==> -3

Run = left 1 unit ==> -1

Slope = -3/(-1) ==> 3

So, the equation of the given line is

 y = 3x + 4

Taking one of the point from the shaded region and applying in the equation, we get

(-2, 1)

1 = 3(-2) + 4

1 = -6 + 4

1 = -2

Here -2 is less than 1, so we have to choose the > instead of equal sign in the equation y > 3x + 4

In the given graph, since it is solid line, we have to use ≥ sign.

Hence, the required inequality is

y ≥ 3x + 4

Problem 4 :

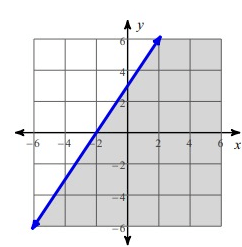
Solution :

Rise = 3 and Run = 2

Slope = 3/2

y- Intercept = 3

So, the equation of the given line is

y = 3/2x + 3

Take the point (2, 2) and apply it in the equation

y = 3/2x + 3

2 = 3/2(2) + 3

2 = 3 + 3

2 = 6

Here 2 is less than 6, so we have to choose the < instead of equal sign in the equation y = 3/2x + 3.

Hence, the required inequality is

y < (3/2)x + 3

Problem 5 :

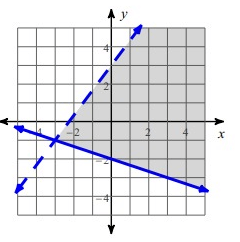
Solution :

Rise = 4 and Run = 3

Slope = 4/3

y- Intercept = 3

So, the equation of the given line is

y = 4/3x + 3

Take the point (3, 3) and apply it in the equation

y = 4/3x + 3

3 = 4/3(3) + 3

3 = 4 + 3

3 = 7

Here 3 is less than 7, so we have to choose the < instead of equal sign in the equation y = 4/3x + 3.

y < 4/3x + 3

Rise = -2 and Run = 6

Slope = -2/6 = -1/3

y- Intercept = -2

So, the equation of the given line is

y = -(1/3)x - 2

Take the point (3, 1) and apply it in the equation

y = -(1/3)x - 2

1 = -(1/3)(3) - 2

1 = -1 - 2

1 = -3

Here 1 is greater than -3, so we have to choose the ≥ instead of equal sign in the equation y = -1/3x - 2.

y ≥ -1/3x - 2

Hence, the required inequality is

y < 4/3x + 3

y ≥ -1/3x - 2

Problem 6 :

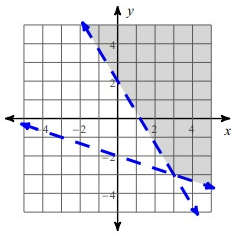
Solution :

Rise = -2 and Run = 1

Slope = -2/1 = -2

y- Intercept = 2

So, the equation of the given line is

y = -2x + 2

Take the point (3, 2) and apply it in the equation

y = -2x + 2

2 = -2(3) + 2

2 = -6 + 2

2 = -4

Here 2 is greater than -4, so we have to choose the > instead of equal sign in the equation y = -2x + 2.

y > -2x + 2

Rise = -2 and Run = 5

Slope = -2/5

y- Intercept = -2

So, the equation of the given line is

y = -2/5x - 2

Hence, the required inequalities are

y > -2x + 2

y = -(2/5)x - 2