WRITE A LINEAR FUNCTION FROM A TABLE

Look for a pattern in the table. Then write an equation that represents the table.

Problem 1 :

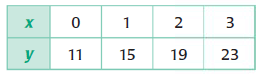
Solution :

Let the linear function, y = mx + b -----(1)

If x = 0 and y = 11, y-intercept(b) is 11.

From the table, the points are (1, 15) and (2, 19).

Slope (m) = (y₂ - y₁)/(x₂ - x₁)

m = (19 - 15)/(2 - 1)

m = 4/1

m = 4

By applying the value of m and b, we get

y = 4x + 11

Problem 2 :

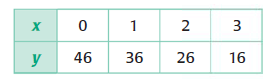
Solution :

Let the linear function, y = mx + b -----(1)

If x = 0 and y = 46, y-intercept(b) is 46.

From the table, the points are (1, 36) and (2, 26).

Slope (m) = (y₂ - y₁)/(x₂ - x₁)

m = (26 - 36)/(2 - 1)

m = -10/1

m = -10

By applying the value of m and b, we get

y = -10x + 46

Problem 3 :

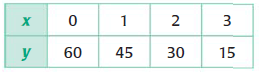
Solution :

Let the linear function, y = mx + b -----(1)

If x = 0 and y = 60, y-intercept(b) is 60.

From the table, the points are (1, 45) and (2, 30).

Slope (m) = (y₂ - y₁)/(x₂ - x₁)

m = (30 - 45)/(2 - 1)

m = -15/1

m = -15

By applying the value of m and b, we get

y = -15x + 46

Problem 4 :

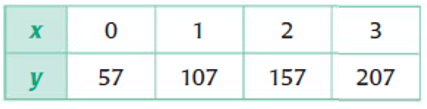
Solution :

Let the linear function, y = mx + b -----(1)

If x = 0 and y = 57, y-intercept(b) is 57.

From the table, the points are (1, 107) and (2, 157).

Slope (m) = (y₂ - y₁)/(x₂ - x₁)

m = (157 - 107)/(2 - 1)

m = 50/1

m = 50

By applying the value of m and b, we get

y = 50x + 57

Problem 5 :

Which equation represents the table at the right ?

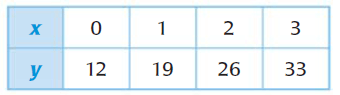
(a) y = 5x + 7   (b) y = 7x + 5

(c) y = 12x - 5   (d)  y = 7x + 12

Solution :

Let the linear function, y = mx + b -----(1)

If x = 0 and y = 12, y-intercept(b) is 12.

From the table, the points are (1, 19) and (2, 26).

Slope (m) = (y₂ - y₁)/(x₂ - x₁)

m = (26 - 19)/(2 - 1)

m = 7/1

m = 7

By applying the value of m and b, we get

y = 7x + 12

So, option D is correct.

Problem 6 :

The first story of a building is 24 feet high, and each additional story is 18 feet high. Write an expression for the height to the top of the nth story. Explain the meaning of each term in the expression.

Solution :

Height of the building  = 24 feet

Height of each additional story(m) = 18 feet

y = mx + b 

y = 18x + 24

Problem 7 :

A website hosting company charges an initial fee of $48 to set up a website. The company charges $44 per month to maintain the website.

a. Write a linear model that represents the total cost of setting up and maintaining a website as a function of the number of months it is maintained.

b. Find the total cost of setting up a website and maintaining it for 6 months.

c. A different website hosting company charges $62 per month to maintain a website, but there is no initial set-up fee. You have $620. At which company can you set up and maintain a website for the greatest amount of time? Explain.

Solution :

Set up fee = $48

Charge per month = $44

Let y be the total cost and x be the number of months maintaining the website.

a)  y = 48 + 44x

b)  When number of months = 6

y = 48 + 44(6)

= 48 + 264

= $312

c) Another company offers = $62 per month

Number of months we can maintain the website in different company = 620/62

= 10 months

Number of months we can maintain the website in the first company :

620 = 48 + 44x

620 - 48 = 44x

572 = 44x

x = 572/44

x = 13

So, the first company offers the best deal.

Problem 8 :

A T-shirt design company charges your team an initial fee of $25 to create the team's design. Each T-shirt printed with your design costs an additional $8.

a. Write a linear model that represents the total cost of purchasing your team’s T-shirts with your design as a function of the number of T-shirts.

b. Your team has 35 members. If a T-shirt is purchased for every member, what would be the cost?

Solution :

Initial fee = $25

Additional cost = $8 per T-shirt

a)  Let y be the total cost and x be the number of T-shirts

y = 25 + 8x

b)  Number of T-shirts to be purchased = 35

y = 25 + 8(35)

= 25 + 280

y = 305

Problem 9 :

You pay a processing fee and a daily fee to rent a beach house. The table shows the total cost of renting the beach house for different numbers of days

a. Can the situation be modeled by a linear equation? Explain.

b. What is the processing fee? the daily fee?

c. You can spend no more than $1200 on the beach house rental. What is the maximum number of days you can rent the beach house?

Solution :

a)  Finding slope, using the points (2, 246) (4, 450) and (6, 654).

Since the slopes are equal, it may create a linear model.

b) y = mx + b

y = 102x + b

Applying the point (6, 654), we get

654 = 102(6) + b

654 = 612 + b

b = 654 - 612

b = 42

y = 102x + 42

Daily fee = $102

Processing fee = $42

c) y = 1200

1200 = 102x + 42

1200 - 42 = 102x

1158 = 102x

x = 1158 / 102

x = 11.35

Approximately 11 days.