WRITE THE INVERSE VARIATION FUNCTION FOR THE GIVEN VALUES OF X AND Y

The variables x and y vary directly. Use the values to write an equation that relates x and y.

Problem 1 :

y = 4; x = 2

Solution :

Direct variation :

y = ax ----(1)

Here a is constant of variation.

Applying x = 2 and y = 4, we get

4 = a(2)

2a = 4

a = 2

Applying the value of a in (1), we get

y = 2x

Problem 2 :

y = 25; x = 5

Solution :

Direct variation :

y = ax ----(1)

Here a is constant of variation.

Applying x = 5 and y = 25, we get

25 = a(5)

5a = 25

a = 5

Applying the value of a in (1), we get

y = 5x

Problem 3 :

y = 60; x = 15

Solution :

Direct variation :

y = ax ----(1)

Here a is constant of variation.

Applying x = 15 and y = 60, we get

60 = a(15)

15a = 60

a = 4

Applying the value of a in (1), we get

y = 4x

Problem 4 :

Write a direct variation equation that relates x inches to y centimeters.

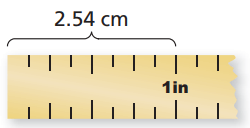
Solution :

Here 2.54 cm = 1 inch

When x = 1 inch, y = 2.54 cm

When x = 2 inch, y = 2(2.54) ==> 5.08

Constant of variation is 2.54

y = ax

y = 2.54 x

Problem 5 :

The weight of an object in our solar system varies directly with the weight of the object on Earth.

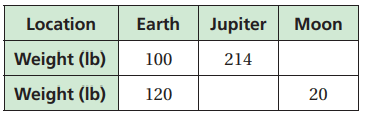
a) Complete the table

Solution :

Let E, J and M be the weights on Earth, Jupiter and Moon respectively.

E ∝ J

E = kJ

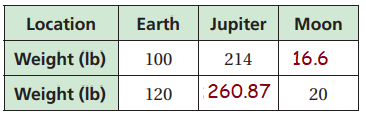
Finding the missing value for Jupiter :

If E = 100, J = 214

100 = k(214)

k = 100/214

k = 0.46

Applying the value of constant of variation.

E = 0.46 J

When E = 120, J = ?

120 = 0.46(J)

J = 120/0.46

J = 260.87

Finding the missing value for Moon :

E ∝ M

E = kM

If E = 120, M = 20

120 = k(20)

k = 120/20

k = 6

Applying the value of constant of variation, we get

E = 6M

When E = 100, M = ?

100 = 6(M)

100/6 = M

M = 16.6

Problem 6 :

Tell whether x and y show direct variation. If so, write an equation of direct variation.

Solution :

If x = 500, y = 40

Checking the relationship for x and y:

y = ax

40 = 500a

a = 40/500

a = 2/25 ----(1)

If x = 700, y = 50

50 = 700a

a = 50/700

a = 1/14----(2)

Constant of variation is not equal, then it is not direct variation.

Problem 7 :

The amount of chlorine in a swimming pool varies directly with the volume of water. The pool has 2.5 milligrams of chlorine per liter of water. How much chlorine is in the pool?

Solution :

Let C be the quantity of chlorine and gallon of water be G.

When C = 2.5 milligram, G = 1000 gallons

C directly varies to G, then 

C = k G

k is the constant of variation.

2.5 = k (1000)

k = 2.5/1000

k = 0.0025

Applying the value of k, we get

C = 0.0025 G

When G = 8000 gallons, C = ?

C = 0.0025 (8000)

C = 20 milligrams.