WORKSHEET ON APPLICATIONS OF DERIVATIVES FOR AP CALCULUS

Problem 1 :

If y = x sin x, then dy/dx

A)  sin x + cos x       B)  sin x + x cos x      C)  sin x - x cos x

D)  x(sin x + cos x)       E)  x(sin x - cos x)

Solution

Problem 2 :

Let f be the function given by f(x) = 300x - x³. On which intervals is the function f increasing ?

A)  (-∞, -10] and [10, ∞)      B)  [-10, 10]     C)  [0, 10] only 

D)  [0, 10√3] only     E)  [0, ∞)

Solution

Problem 3 :

If f(x) = 7x - 3 + ln x, then f'(1) = ?

A)  4     B)  5      C)  6    D)  7     E)  8

Solution

Problem 4 :

Solution

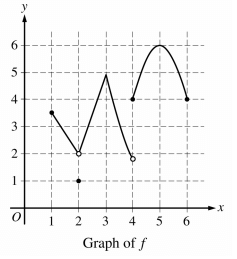
Problem 5 :

If y = (x³ - cos x)⁵, then find y'

A)  5(x³ - cos x)⁴            B)  5(3x² + sin x )⁴ 

C)  5(3x² + sin x)         D)  5(3x² + sin x)⁴ (6x + cos x)

E)  5(x³ - cos x)⁴ (3x² + sin x)

Solution

Problem 6 :

If

f(x) = √(x²-4) and g(x) = 3x-2

then find the derivative of f((g(x)) at x = 3

A)  7/√5     B)  14/√5      C)  18/√5    D)  15/√21     E)  30/√21

Solution

Problem 7 :

The function f is defined by f(x) = x/(x + 2). What points (x, y) on the graph of f have the property that the line tangent to f at (x, y) has slope 1/2 ?

A)  (0, 0) only       B)  (1/2, 1/5) only     C)  (0, 0) and (-4, 2)

D)  (0, 0) and (4, 2/3)    E) There are no such points

Solution

Problem 8 :

Let f(x) = (2x+1)³ and let g be the inverse function of f. Given that f(0) = 1, what is the value of g'(1) ?

A)  -2/27      B)  1/54    C)  1/27   D)  1/6    E)  6

Solution

Problem 9 :

Let f be the function defined by f(x) = ln x/x. What is absolute maximum value of f ?

A)  1    B)  1/e      C)  0       D) -e

E) f does not have an absolute maximum value

Solution

Problem 10 :

Let g be the function given by g(x) = x² e^kx, where k is a constant. For what value of k does g have critical point at x = 2/3 ?

A)  -3    B)  -3/2    C)  -1/3      D)  0     E) There is no such k.

Solution