WORD PROBLEMS ON SURFACE AREA OF CONE

What is cone ?

A cone is a three-dimensional shape in geometry that narrows smoothly from a flat base (usually circular base) to a point(which forms an axis to the center of base) called the apex or vertex.

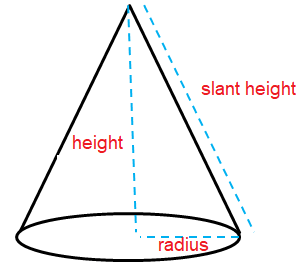
To find lateral surface area and total surface area of cone, we use the formulas given below.

Lateral surface area =  πrl

Total surface area =  πrl +  πr²

= πr(l + r)

l = √r² + h²

Here r = radius, l = slant height

Problem 1 :

Total surface area of a cone whose radius as p/2 and slant height as 2l is:

(a) 2πp(l + p)                       (b) πp(l + (p/4))

(c)  πp(l + p)                         (d) 2πpl

Solution :

Total surface area of cone = πr(l+r)

r = p/2 and l = 2l

Problem 2 :

If the slant height of a cone 12 cm and radius of the base is 14 cm, then the total surface area is.

Solution :

Slant height (l) = 12 cm, radius (r) = 14 cm

Total surface area = πr(l+r) 

Problem 3 :

The radius and height of a cone are in the ratio 4:3. The area of the base is 154 cm². Find the curved surface area

Solution :

Radius : height = 4 : 3

Radius = 4x and height = 3x

Area of the base = 154 cm²

πr² = 154

(22/7)r² = 154

r² = 154(7/22)

r² = 49

r = 7

4x = 7, then x = 7/4

height = 3(7/4) ==> 21/4 ==> 5.25

l = √7² + (5.25)²

l = √49 + 27.56

l = √76.56

l = 8.75

Curved surface area = πrl

= (22/7) . 7. (8.75)

= 192.5 cm²

Problem 4 :

There are two cones, the curved surface area of one cone is twice that of the other. The slant height of later is twice that of the former. Find the ratio of their radii.

Solution :

Curved surface area of one cone = 2 curved surface area of other

Let r₁ and l₁ be the radius and slant height of one cone

Let r₂ and l₂ be the radius and slant height of other cone

πr₁l₁= 2(πr₂l₂)  ---(1)

l₂ = 2l₁

By applying the value of L in (1), we get

πr₁l₁ = 2(πr₂(2l₁))

r₁ = 4r₂

r₁/r₂ = 4 : 1

Ratio of their radii is 4 : 1.

Problem 5 :

How much material is needed to make the Nón Lá Vietnamese leaf hat? Find the height.

Solution :

Diameter = 20 inches, radius = 10 inches

Slant height = 13 inches

l² = r² + h²

13² = 10² + h²

h² = 169 - 100

h² = 69

h = √69

h = 8.3 inches

Surface area of cone = πrl

= 3.14 x 10 x 13

= 408.2 square inches

Problem 6 :

A paper cup shaped like a cone has a diameter of 6 centimeters and a slant height of 7.5 centimeters. How much paper is needed to make the cup?

Solution :

Slant height = 7.5 cm

Diameter = 6 cm, radius = 3 cm

Surface area of cone shaped cup = πrl

= 3.14 x 3 x 7.5

= 70.65 square inches

Problem 7 :

The total surface area of the cone is 100𝛑 square meters and radius is 5 m. What is the slant height of the cone.

Solution :

surface area of the cone = πrl + 2πr²

πrl + 2πr² = 100𝛑 

πr(l + 2r) = 100𝛑 

5(l + 2(5)) = 100

5(l + 10) = 100

l + 10 = 100/5

l + 10 = 20

l = 20 - 10

l = 10 m

Problem 8 :

A right cone has a base radius of 4 m and a height of 10 m. Calculate the surface area of this cone to the nearest square meter.

Solution :

Radius = 4 m, height = 10 m

Surface area = πrl

l² = r² + h²

l² = 4² + 10²

l² = 16 + 100

l² = 116

l = √116

l = 10.77 m

Surface area = 3.14 x 4 x 10.77

= 135.2712 square meter

Problem 9 :

Aiden built a cone-shaped volcano for a school science project. The volcano has a base diameter of 32 cm and a slant height of 45 cm.

a) What is the lateral area of the volcano to the nearest tenth of a square centimeter?

b) The paint for the volcano’s surface costs $1.99 jar, and one jar of paint covers 400 cm². How much will the paint cost?

Solution :

Radius = 32 cm, slant height = 45 cm

a)

Lateral surface area = πrl

= 3.14 x 32 x 45

= 4521.6 cm²

b)

1 jar of paint covers = 400 cm²

Number of jars required = 4521.6/400

= 11.304

Approximately 12 jars.

Total cost = 12 x 1.99

= $23.88