WORD PROBLEMS ON SQUARE ROOTS

Problem 1 :

Landscaping Read wants to have a square garden plot in his backyard. He has enough compost to cover an area of 75 square feet. How long can a side of his garden be?

Solution :

Let ‘s’ be the side length of the square.

Area of the square = s²

Area of the square garden = 75 square feet

75 = s²

To find the value of s, take square roots on both sides.

s = √75

s = 8.66

So, the side length of the garden is 8.66 feet.

Problem 2 :

Landscaping Read wants to have a square garden plot in his backyard. He has enough compost to cover an area of 130 square feet. How long can a side of his garden be?

Solution :

Let ‘s’ be the side length of the square.

Area of the square = s²

Area of the square garden = 130 square feet

130 = s²

To find the value of s, take square roots on both sides.

s = √130

s = 11.402

So, the side length of the garden is 11.402.

Problem 3 :

Decorating Denise wants to install a square accent of designer tiles in her new shower. She can afford to buy 625 square centimeters of designer tiles. How long can a side of the accent be? 

Solution :

Let A be a square centimeters = 625 

Area of the square = s²

 625 = s²

s = √625

s = 25

So, the side length of the accent is 25.

Problem 4 :

Decorating Morris wants to have a square mosaic inlaid in his new patio. His budget allows for 2,025 tiles. Each tile is square with an area of one square inch. How long can a side of the mosaic be? 

Solution :

Let A be a square with an area = 2,025

Area of the square = s²

s = √2025

s = 45

So, the side length of the mosaic is 45.

Problem 5 :

Amber wants to put carpet on the floor of her bedroom. The floor is a square with an area of 182.25 square feet. How long should the piece of carpet be on each side?

Solution :

Area of a square of the floor = 182.25 square feet.

Let s be the side of the piece of carpet.

Area of the square = s²

182.25 = s²

s = √(182.25)

s = 13.5 feet

Problem 6 :

A square has a side length of 3x and an area of 324 in². What is the value of x ?

Solution :

Area of  square (A) = 324 in²

Length of the side (s) = 3x

Area of the square = s²

 324 = (3x)²

324 = 9x²

(324)/9 = x²

36 = x²

x = √36

x = 6

So, the value of x is 6.

Problem 7 :

The area of a square is 144 cm². What is the length of one side?

Solution :

Area of a square = 144 cm²

Length of one side = ?

Area of the square = s²

144 = s²

s = √144

s = 12 cm

So, the length of one side is 12 cm.

Problem 8 :

The area of a square is 289 m². What is the perimeter of the square?

Solution :

Area of a square = 289 m²

Let a be the side.

Area of the square = a²

289 = a²

a = √289

a = 17

To find the perimeter of the square,

Perimeter = 4a

P = 4(17)

P = 68

Problem 9 :

In an auditorium, the number of rows is equal to the number of chairs in each row. If the capacity of the auditorium is 2025, find the number of chairs in each row.

Solution :

Let x be the number of rows and number of columns.

Capacity of the auditorium = 2025

x ⋅ x = 2025

x² = 2025

x = √2025

x = √(5 ⋅ 3 ⋅ 3 ⋅ 5)

= 5 ⋅ 3

x = 15

So, the number of rows and number of columns is 15.

Problem 10 :

Find the smallest number by which 9408 must be divided so that the quotient is a perfect square.

Solution :

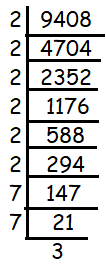
= √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 7 ⋅ 7 ⋅ 3)

9408 should be divided by 3 to make it as perfect square.

Problem 11 :

The area of square field is 49284 m². Find the cost of fencing the field at $15 per metre.

Solution :

Area of square field = 49284 m²

Let x be the side length of square.

x² = 49284

x = √49284

x = 222

Perimeter of square field = 4x

= 4(222)

= 888 m

Cost of fencing per meter = $15

Total cost = 888 (15)

= $13320

Problem 12 :

Each member of a picnic party contributed twice as many dolars as the total number of members and the total collection was dollars 3042. Find the number of members present in the party.

Solution :

Let x be the amount in dollars.

Number of members = 2x

2x(x) = 3042

2x² = 3042

x² = 3042/2

x² = 1521

x = √1521

x = 39

So, the number of members in the party is 2(39), that is 78.