WORD PROBLEMS ON SQUARE AND SQUARE ROOTS

Problem 1 :

1225 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.

Solution :

Number of plants in each row = number of rows

Number of plants in each row = x

Total number of plants = 1225

number of plants in each row ⋅ number of rows = x²

x² = 1225

x = √1225

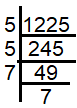
x = √(5 ⋅ 5 ⋅ 7 ⋅ 7)

x = 5 ⋅ 7 

x = 35

So, number of plants in each row = 35, number of rows = 35 rows.

Problem 2 :

Find the smallest number by which 3645 should be divided so as to get a perfect square. Also, find the square root of the number so obtained.

Solution :

From the given information 3645 is not a perfect square.

3645 should be divided by some small number to make it as perfect square. To find the smallest number, we try to write 3645 as product of prime factors.

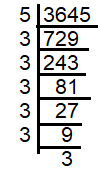
√3645 = √(5 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3)

After grouping them as pairs, we get one 5 as extra. So, that is the value should be ignored to make it as perfect square.

3645 should be divided by 5 to make it as perfect square.

3645/5 = 729

√729 = √(3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3)

= 3 ⋅ 3 ⋅ 3

= 27

Problem 3 :

For each of the following numbers, find the smallest number by which we divide it so as to get a perfect square. Also find the square root of the square numbers so obtained.

a)  37845           (b) 2800             (c) 45056

Solution :

Using prime factorization method, we write 37845 as product of prime factors.

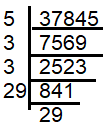
√37845 = √(5 ⋅ 3 ⋅ 3 ⋅ 29 ⋅ 29)

After grouping them as pairs, we get 5 as extra. So, 37845 should be divided by 5 to make it as perfect square.

Number obtained by dividing the given number by 5 :

37845/5 = 7569

√7569 = √(3 ⋅ 3 ⋅ 29 ⋅ 29)

= 3 x 29

= 87

(b) 2800

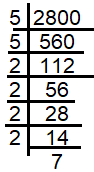
√2800 = √(5 ⋅ 5 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 7)

After grouping them as pairs, we get 7 as extra. So, 2800 should be divided by 7 to make it as perfect square.

Number obtained by dividing the given number by 7 :

2800/7 = 400

√400 = √(5 ⋅ 5 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2)

= 5 x 2 x 2

= 20

(c) 45056

√45056 = √(2¹² x 11)

After grouping them as pairs, we get 11 as extra. So, 45056 should be divided by 11 to make it as perfect square.

Number obtained by dividing the given number by 11 :

45056/11 = 4096

√4096 = √(2¹²)

= 2⁶

= 64

Problem 4 :

The students of Class VIII of a school donated $2401 for Relief Fund. Each student donated as many dollars as the number of students in the Class. Find the number of students in the Class.

Solution :

Amount donated by each student = number of students in the class

Amount donated = 2401

Let x be the amount donated by each student and number of students in the class.

x ⋅ x = 2401

x² = 2401

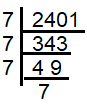
x = √2401

x = √(7 ⋅ 7 ⋅ 7 ⋅ 7)

= 7 ⋅ 7

x = 49

Problem 5 :

There are 500 children in a school. For a P.T. drill they have to stand in such a manner that the number of rows is equal to number of columns. How many children would be left out in this arrangement?

Solution :

Number of children in a school = 500

Number of rows = number of columns

Let x be the number of rows, then number of columns will also be x.

x (x) = total number of students will be in the arrangements

Finding the square root of the given number,

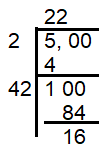
The nearest perfect square number for 500 is 22² = 484

Difference between 484 and 500, we get

= 500 - 484

= 16

So, after standing up the students in 22 rows in which each row consists of 22 students, there must be 16 students left over.