WORD PROBLEMS ON PERIMETER OF 2D SHAPES

Problem 1 :

A farmer decides to fence a 400 m by 350 m field with a 4-strand wire fence. Find :

a) The perimeter of the field

b)  The total length of wire required

c) The total cost of wire required if a single strand of wire costs 12.4 cents per metre.

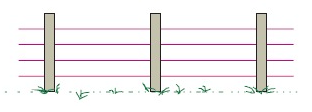
Solution :

Length = 400 m and width = 350 m

a) Perimeter = 2(length + width)

= 2(400 + 350)

= 2(750)

= 1500 m

b) Total length = 4(1500)

= 6000 m

c) Total cost = 12.4 × 6000

= $ 74400

Problem 2 :

Boxes containing computers are fastened with three pieces of tape, as shown.

Each piece of tape is overlapped 5 cm at the join. Calculate the total length of tape required for 20 boxes.

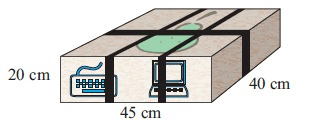
Solution :

Length of tape for 1 box = 2(45 + 20) + 4(40 + 20) + 15

= 130 + 240 + 15

= 385 cm

Length for 20 boxes = 20 × 385

= 7700 cm

= 7700 × 0.01

= 77 m

So, total length for 20 boxes is 77 m.

Problem 3 :

The minute hand of a clock is 8 cm long. How far does the tip travel between 2.00 pm and 2.45 pm?

Solution :

Difference = 2.45 - 2.00 = 45 min

The minute hand moves through 2π × 45/60

= 3π/2 radians

Since the length of the minute hand is 8 cm, the distance moved by the tip of the hand is given by the formula,

l = r θ

= 8 × 3π/2

= 24π/2

= 12π cm

= 12 × 3.14

= 37.7 cm

Problem 4 :

Which is the shorter path from A to B :

Around the 2 smaller semi-circles or around the large semi-circle?

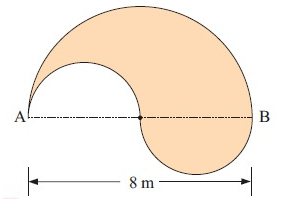
Solution :

The distance around the large semi circle

= 1/2 × π × diameter

= 1/2 × 8 × π

= 4π m

The distance around the 2 smaller semi circles

= 1/2 × 4 × π + 1/2 × 4 × π

= 2π + 2π

= 4π m

Both are same.

Problem 5 :

A machine makes circular paper plates which have circumference 50 cm. find the diameter of a plate correct to the nearest mm.

Solution :

Given, circumference = 50 cm

Circumference = 2πr

d = 2r

d = C/π

d = 50/3.14

d = 15.9 cm

Problem 6 :

A bicycle wheel has diameter 0.6 m.

a) Find the circumference of the wheel to the nearest mm.

b) Through how many revolutions must the wheel turn during a 100 km trip?

Solution :

a) Given, diameter = 0.6 m

d = C/π

C = π × d

C = 3.14 × 0.6

C = 1.884 m

b) 100 km = 100000 m

= 100000/1.884

≈ 53078 revolutions

Problem 7 :

a)   Find the perimeter P of the figure alongside, giving your answer in simplest form.

b)   If the perimeter of the figure is 30 cm:

i)  Find x

ii)  Find the length of the longest side.

Solution :

Given, perimeter = 30 cm

i)  x - 2 + 2x - 3 + x + 4 + x + 4 + 7 = 30

5x + 10 = 30

5x = 30 - 10

5x = 20

x = 4

ii) Length of longest side = x + 4 cm

= 4 + 4

= 8 cm

Problem 8 :

Length of a rectangular field is 220 m and width is 130 m. If a man runs around this field 3 times, find the distance covered by him?

Solution :

Length of the field = 220 m 

Width = 130 m

Perimeter of the field = 2(220 + 130)

= 2(350)

= 700 m

Distance covered by the man = 3(700)

= 2100 m

Problem 9 :

Rahul walks around a square park once and covers 800 m. What will be the area of the park ?

Solution :

Length around the square park = 800 m

Let a be the side length of the park.

4a = 800

a = 800/4

a = 200

Area of the park = 200²

= 40000 square meter

Problem 10 :

The area of a rectangular field is 1600 sqm. If the length of the field is 80 m, find the perimeter of the field?

Solution :

Area of the rectangular field = 1600 sq.m

Length = 80 m

Let width be a.

Length x a = 1600

80a = 1600

a = 1600/80

a = 20

Width of the rectangular field = 20 m

Perimeter = 2(length + width)

= 2(80 + 20)

= 2(100)

= 200 meter

Problem 11 :

ABCD is a parallelogram in which AE is perpendicular to CD. Also AC = 5 cm, DE = 4 cm, and the area of ∆ AED = 6 cm². Find the perimeter and area of ABCD

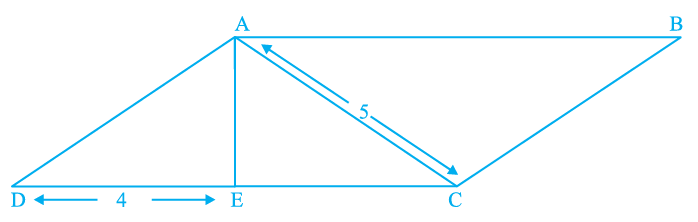
Solution :

Area of triangle AED =  6 cm²

1/2 x DE x AE = 6

1/2 x 4 x AE = 6

2(AE) = 6

AE = 3 cm

EC² + AE² = AC²

EC² + 3² = 5²

EC² + 9 = 25

EC² = 25 - 9

EC² = 16

EC = 4 cm

Since it is parallelogram, the opposite sides are equal.

DC = DE + EC

= 4 + 4

DC = 8 cm

In triangle AED,

DE² + AE² = AD²

4² + 3² = AD²

AD² = 16 + 9

AD² = 25

AD = 5

Perimeter of the parallelogram = 2(5 + 3 + 4)

= 2(12)

= 24 cm