WORD PROBLEMS ON LEAST COMMON MULTIPLE

Problem 1 :

At the gym, Hillary swims every 6 days, runs every 4 days, and cycles every 16 days. If she did all three activities today, in how many days will she do all three activities again on the same day?

Solution :

The days on which Hillary swims in the following cycle :

6, 12, 18, 24, .............

The days on which Hillary runs in the following cycle :

4, 8, 12, 16, ...........

The days on which Hillary swims in the following cycle :

16, 32, 48, ...............

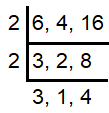
= 2 x 2 x 3 x 1 x 4

= 48

So, after 48 days he will do everything on same day.

Problem 2 :

Cups are sold 6 to a package and plates are sold 8 to a package. If you want to have the same number of each item for a party, what is the least number of packages of each you need to buy?

Solution :

Number of cups in a package = 6

Number of plates in a package = 8

To choose the same number of package in each case, we find the least common multiple.

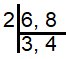
Least common multiple of (6, 8) is = 2 x 3 x 4

= 24

Problem 3 :

Boxes that are 12 inches tall are being piled next to boxes that are 10 inches tall. What is the least height in feet at which the two piles will be the same height?

Solution :

Height of first box = 12 inches

height of second box = 10 inches

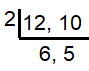
Least common multiple = 2 x 6 x 5

= 60

So, with the height of 60 inches two piles will reach the same height.

Problem 4 :

A manager at a restaurant can buy hamburger buns in packages of 8 and hamburger patties in packages of 6. Suppose that the manager cannot buy part of a package. What is the least number of packages of each product he can buy to have an equal number of hamburger patties and buns? 

Solution :

Available in once packet :

Number of ham burger buns = 8

Number of hamburger patties = 6

To have equal number of hamburger bun and patties, we find

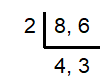
= 2 x 4 x 3

= 24

Problem 5 :

Two men running a marathon took a sip of water at the same time 72 minutes after they started the race. If the first man took a sip of water every 9 minutes, how often did the other man take a sip of water?

Solution :

From the given information, it is clear the least common multiple is 72 minutes.

The first man took a sip after 9 seconds.

The second man took a sip after = 72/9

= 8 seconds

Problem 6 :

Steve can save 9 dollars every day while Maria can save 12 dollars every day. What is the least number of days it will take each person to save the same amount of money?

Solution :

Amount saves by Steve = $9

Amount saves by Maria = $12 

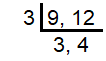
= 3 x 3 x 4

= 36

They will save $36.

Problem 7 :

Henry and Margo both began traveling around a circular track. Henry is riding his bike, and Margo is walking. It takes Henry 7 minutes to make it all the way around, and Margo takes 12 minutes. How much time will pass until they meet at the starting line?

Solution :

Henry will complete covering the circular track in the following minutes.

7, 14, 21, ............

Margo will complete covering the circular track in the following minutes.

12, 24, 36, ..........

Least common multiple of 7 and 12 is 84.

So, they will meet each other at the starting line after 84 minutes.

Problem 8 :

At the movie theatre, they give out a free drink to every 75th customer and a free bag of popcorn to every 30th customer. On Monday 3,000 customers came to the theatre. How many people received both free items?

Solution :

Every 75th customer will get free drink

Every 30th customer will get popcorn.

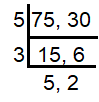
= 3 x 5 x 5 x 2

= 150

Every 150th customer will get both. To find the number of customer to get both

= 3000 / 150

= 20

So, out of 3000 customers 20 customers will get both.

Problem 9 :

Melanie has pieces of train track that are 8 inches long that she is connecting together to form a track that her train can travel on. Martin is also trying to construct a track for his train but is using track pieces that are 20 inches long. How long will the shortest track be if the track that Melanie builds ends up being the same length as Martin’s track?

Solution :

Length of Melanie's train track = 8 inches

Length of  Martin's train track = 20 inches

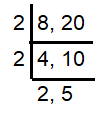
= 2 x 2 x 2 x 5

= 40

Length is 40 inches.

Problem 10 :

Radio station Z-100 was giving away $100 bill to every 100th caller during a contest and gave Jingle ball tickets to every 40th caller. How many caller must call before someone wins both a $100 bill and Jingle ball ticket ?

Solution :

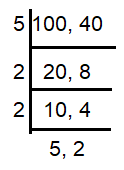
= 5 x 2 x 2 x 5 x 2

= 200 callers