WORD PROBLEMS ON DIRECTION AND DISTANCE

Problem 1 :

A car travels 9 km due to north and then 12 km due west. How far is the car from its starting point ?

Solution :

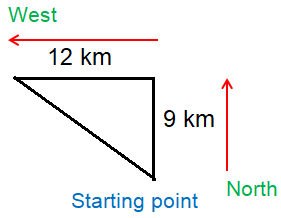
Distance from the starting point to destination :

Let A be the starting point and C be the destination.

The triangle is the right triangle, using Pythagorean theorem

AC² = 12² + 9²

= 144 + 81

AC² = 225

AC = √225

AC = 15

Problem 2 :

The cyclist is 32 km east and 18 km south of her starting point. She wants to return to her starting point in a direct line.

a) How far is the cyclist in a direct line from her starting point ?

b)  How long will it take to her to return to her starting point if she can ride at 36 km per hour ?

Solution :

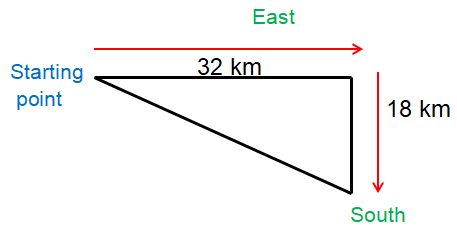
a) Let A be the starting point and C be the destination.

The triangle is the right triangle, using Pythagorean theorem

AC² = 32² + 18²

= 1024 + 324

AC² = 1348

AC = √1348

AC = 36.72 km

b) Distance covered = 36.72 km

Speed = 36 km per hour

Time = Distance / speed

= 36.72/36

= 1 hour 1 minute

Problem 3 :

Two trains A and B leave the station at the same time. Train A travels north at a constant speed of 45 km per hour. Train B travels east at a constant speed of 70 km per hour.

a) How far will each train have travelled after 3 hours ?

b) Find the distance between A and B after 3 hours.

Solution :

Distance covered = Time x speed

Each train is travelling for 3 hours.

a)

Distance covered by train A = 45 km per hour

= 45 x 3

= 135 km

Distance covered by train B = 70 km per hour

= 70 x 3

= 210 km

b) 

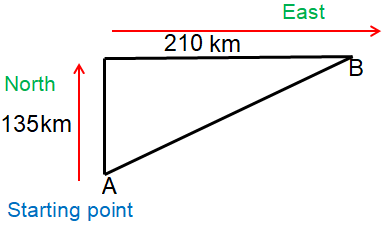
AB² = 135² + 210²

AB² = 18225 + 44100

AB² = 62325

AB = √62325

AB = 249.64

Approximately the distance between A to B is 250 km.

Problem 4 :

Two brothers leave their house at the same time. Alex runs due east at a constant speed of 10 km per hour and Boris walks due south at a constant speed of 4 km per hour.

a) How far has each brother travelled after 30 minutes ?

b) Find the distance between the two brothers after 30 minutes.

Solution :

Time = distance / speed

Distance = time x speed

a) Alex is running at the speed of 10 km per hour.

Distance = (1/2) x 10

= 5 km

Boris is walking at the speed of 4 km per hour.

Distance = (1/2) x 4

= 2 km

b) 

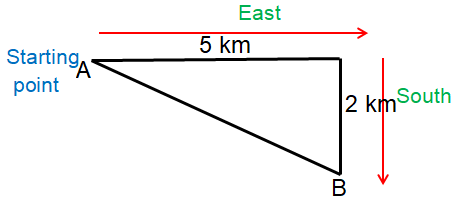
AB² = 5² + 2²

AB² = 25 + 4

AB² = 29

AB = √29

AB = 5.38 km