WORD PROBLEMS ON AREA AND PERIMETER

Problem 1 :

The area of a square is 625 cm². Find the length of the sides.

Solution :

Given, the area of a square = 625 cm².

Area of square = a²

625 = a²

a = √625

a = 25 cm

So, side length is 25 cm. 

Problem 2 :

The area of a rectangle is 600 cm². Find the width of the rectangle if the length is 40 cm.

Solution :

Area of a rectangle = 600 cm²

Length = 40 cm

The area of a rectangle = length × width

600 = 40 × width

Width = 600/40

Width = 15 cm

So, the width of rectangle is 15 cm.

Problem 3 :

The area of a triangle is 45 cm². Find the base of the triangle if the height is 9 cm.

Solution :

Area of a triangle = 45 cm².

Height = 9 cm

The area of a triangle = 1/2 × b × h

45 = 1/2 × b × 9

45 = 4.5 × b

b = 45/4.5

b = 10 cm

So, base of the triangle is 10 cm.

Problem 4 :

The area of the circle is 8π cm². Find the circumference of the circle.

Solution :

Given, the area of the circle = 8π cm²

Area of the circle = πr²

8π = πr²

r² = 8

r = 2.82 cm

Circumference of the circle = 2πr

C = 2π × 2.82

C = 17.70 cm

So, circumference of the circle is 17.70 cm.

Problem 5 :

The area of a square is 400 cm². Find the perimeter of the square.

Solution :

Area of a square = 400 cm²

400 = a²

a = √400

a = 20 cm

Perimeter of the square = 4a

= 4 × 20

= 80 cm

So, perimeter of the square is 80 cm.

Problem 6 :

The perimeter of a rectangle is 30 cm with the length being 8 cm. Find the area of the rectangle.

Solution :

Perimeter of a rectangle = 30 cm

Length = 8 cm

The perimeter of a rectangle = 2(l + w)

30 = 2(8 + w)

30 = 16 + 2w

2w = 30 - 16

2w = 14

w = 7 cm

The area of rectangle = length × width

= 8 × 7

= 56 cm²

So, the area of rectangle is 56 cm².

Problem 7 :

If a rectangle has area of 32 2/3 inch and a length of 14 inch, what is its width?

Solution :

Area of rectangle = 32 2/3 inch

Length = 14 inch

Area of rectangle = length × width

32 2/3 = 14 × width

98/3 = 14 × width

Width = 7/3 inch

So, the width of rectangle is 7/3 inch.

Problem 8 :

If a rectangle has area of 38 inch and a length of 4 ¾ inch, what is its width?

Solution :

Area of rectangle = 38 inch

Length = 4 ¾ inch

Area of rectangle = length × width

38 = 19/4 × width

Width = 38 / (19/4)

Width = 8 inch

So, the width of rectangle is 8 inch.

Problem 9 :

A rectangle field is 48 m long and 20 m wide. How many triangular flower beds whose sides containing right angle measure 12 m and 5 m can be laid on this field ?

Solution :

Length of rectangle = 48 m, width = 20 m

Base of triangle = 12 m and height = 5 m

Number of triangles = Area of rectangle / area of one triangle

= (48 x 20) / (1/2) x 12 x 5

= (48 x 20) / (6 x 5)

= 32 triangular beds

Problem 10 :

The measurements in this given figure are in the cm. What is its are in the cm. What is its area ?

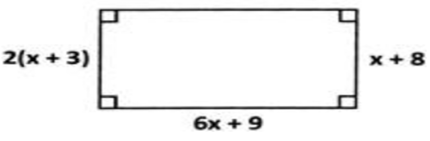
Solution :

Widths are 2(x + 3) and x + 8

2(x + 3) = x + 8

2x + 6 = x + 8

2x - x = 8 - 6

x = 2

Area of rectangle = 21 x 10

= 210 square cm

Problem 11 :

If the perimeter of a square increased by 25% then what is the increase in its area ?

Solution :

Let x be the side length of the square.

Perimeter of square = 4x

Perimeter of new square = 125% of 4x

Let A be the side length of new square.

4A = 125% of 4x

A = 1.25 (4x/4)

A = 1.25 x

= 125% of x

So, the new side length of the square should be increased by 25% of old square.

Problem 12 :

Find the cost of flooring the portico at the rate of $12 per square meter if the length and width of portico are in the ratio of 3 : 2 and its perimeter is 40 m.

Solution :

Length of the rectangle = 3x

Width of the rectangle = 2x

Perimeter = 40

3x + 2x = 40

5x = 40

x = 40/5

x = 8

Length = 3(8) ==> 24 m

Width = 2(8) ==> 16 m

Area of rectangle = 24 x 16

= 384 square meter.

Cost per square meter = $12

Required cost = 384 x 12

= $4608