WORD PROBLEMS INVOLVING THE MAXIMUM OR MINIMUM OF A QUADRATIC FUNCTION

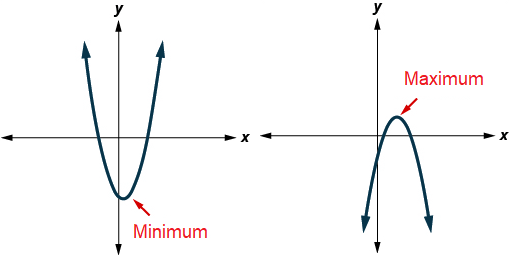
In general the graphical form of the quadratic function will the shape of u. It may be open upward or downward.

• Maximum point is the highest point of the parabolic path.
• Minimum point is the lowest point of the parabolic path.

To find maximum or minimum point of the quadratic equation we follow two ways.

(i) Converting into the vertex form

(ii) Using formula

Problem 1 :

Jason jumped off a cliff into the ocean in Acapulco while vacationing with some friends. His height as a function of time could be modeled by the function

h(t) = -16t² + 16t + 480

where t is the time in seconds and h is the height in feet.

a. How long did it take for Jason to reach his maximum height?

b. What was the highest point that Jason reached?

c. Jason hit the water after how many seconds?

Solution :

Let h(t) = -16t² + 16t + 480

Vertex will be the maximum point or highest point of the parabolic path.

Vertex will be in the form of (x, y).

Here x --> t represents the time and y --> h(t) represents the height.

maximum at x = -b/2a

From the given equation, a = -16, b = 16 and c = 480

x = -16/2(-16) ==> 1/2

a) Jason took 0.5 seconds to reach the maximum height.

When t = 1/2, h(t) = -16(1/2)² + 16(1/2) + 480

= -4 + 8 + 480

= 484 ft

b) The maximum height reached by Jason is 484 ft.

c) He will reach the ground, when h(t) = 0.

-16t² + 16t + 480 = 0

Dividing by -16, we get

t² - t - 30 = 0

(t - 6)(t + 5) = 0

t = 6 and t = -5

So, after 6 seconds Jason hit the water to the ground.

Problem 2 :

If a toy rocket is launched vertically upward from ground level with an initial velocity of 128 feet per second, then its height h after t seconds is given by the equations

h(t) = -16t² + 128t

(if air resistance is neglected).

a. How long will it take for the rocket to return to the ground?

b. After how many seconds will the rocket be 112 feet above the ground?

c. How long will it take the rocket to hit its maximum height?

d. What is the maximum height?

Solution :

a) h(t) = -16t² + 128t

When h(t) = 0

-16t² + 128t = 0

-16t(t - 8) = 0

16t = 0 and t - 8 = 0

t = 0 and t = 8

After 8 seconds, the rocket will return the ground.

b)  h(t) = 112

-16t² + 128t = 112

-16t² + 128t - 112 = 0

Dividing by -16, we get

t² - 8t + 7 = 0

(t - 1)(t - 7) = 0

t = 1 and t = 7

After 1 second the rocket will be at 112 ft.

c) h(t) = -16t² + 128t

Using the completing the square method,

h(t) = -16(t² - 8t)

= -16(t² - 2⋅t⋅4 + 4² - 4²)

= -16[(t - 4)² - 16]

= -16(t - 4)² + 256

(h, k) ==> (4, 256)

The rocket will reach the maximum point in 4 seconds.

d) The maximum height is 256 ft.

Problem 3 :

You want to climb to a ledge that is 20 ft above you. The height of the grappling hook you throw is given by the function

h(t) = – 16t² + 32t + 5

What is the maximum height of the grappling hook? Can you throw it high enough to reach the ledge?

Solution :

h(t) = – 16t² + 32t + 5

= – 16[t² - 2t] + 5

= – 16[(t - 1)² - 1] + 5

= – 16(t - 1)² + 16 + 5

= – 16(t - 1)² + 21

The maximum height is 21 ft.

So, you can reach the ledge.

Problem 4 :

A company finds that if they price their product at $60, they can sell 500 items of it. For every dollar increase in the price, the number of items sold will decrease by 5.

a) Let x be the increase in price from $60. Define the revenue function, R (x) to be the sales revenue that results in such pricing. Find a formula for R (x).

b) What price would guarantee an income of $31,500?

c) Find the price that guarantees the maximum revenue.

d) Find the maximum revenue.

Solution :

Let x be the price increase.

a)  R(x) = (60 + x)(500 - 5x)

b) (60 + x)(500 - 5x) = 31500

30000 - 300x + 500x - 5x² = 31500

- 5x²+ 200x  + 30000 - 31500 = 0 

- 5x²+ 200x - 1500 = 0 

x²- 40x + 300 = 0 

(x - 10)(x-30) = 0

x = 10 and x = 30

c) Maximum revenue :

R(x) = (60 + x)(500 - 5x)

= 30000 - 300x + 500x - 5x²

= - 5x² + 200x + 30000

c) The required price is $20.

d) Maximum revenue is 32000.