WORD PROBLEMS INVOLVING DEPRECIATION

Problem 1 :

A car was purchased for $32500 and depreciated annually by 16%. Find its value after 10 years.

Solution:

F_v = P_v (1 - i)ⁿ

= 32500 (1 - 0.16)¹⁰

= 32500 × (0.84¹⁰)

= 32500 × 0.1749

= $5684.29

Problem 2 :

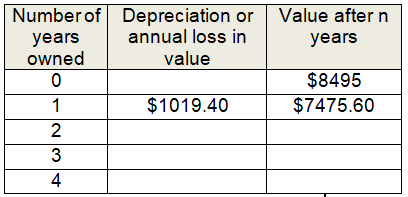
A motorbike was purchased for $8495 in July 2001 and depreciates at 12% each year. Copy and complete the following table:

a. For taxation purposes, the motorbike is essential for making an income (as it is used exclusively in a delivery service). Annual loss in value (called depreciation) can be used as a tax deduction. How much can be 'claimed' during the 4th year of use?

b. Find the value of the motorbike at the end of the 8th year.

c. What is the significance of F₁₀ - F₉?

Solution:

F_v = P_v (1 - i)ⁿ

Number of years owned = 1

Depreciation or annual loss in value = 0.12 × 8495

= $1019.40

F₁ = 8495 (1 - 0.12)¹

= 8495 (0.88)

= $7475.60

Number of years owned = 2

Depreciation or annual loss in value = 0.12 × 7475.60

= $897.07

F₂ = 8495 (1 - 0.12)²

= 8495 (0.88)²

= $6578.53

Number of years owned = 3

Depreciation or annual loss in value = 0.12 × 6578.53

= $ 789.42

F₃ = 8495 (1 - 0.12)³

= 8495 (0.88)³

= $5789.11

Number of years owned = 4

Depreciation or annual loss in value = 0.12 × 5789.11

= $694.69

F₄ = 8495 (1 - 0.12)⁴

= 8495 (0.88)⁴

= $5094.42 

a.

= $1019.40 + $897.07 + $789.42 + $694.69

= $3400.58

b.

F_v = P_v (1 - i)ⁿ

P = 8495, n = 8

F_v = 8495 (1 - 0.12)⁸

= 8495 (0.88)⁸

= 8495 (0.3596)

= 3055.10

c.

F_v = P_v (1 - i)ⁿ

F₁₀ = 8495 (1 - 0.12)¹⁰

= 8495 (0.88)¹⁰

= 8495 (0.2785)

F₁₀ = 2365.86

F₉ = 8495 (1 - 0.12)⁹

= 8495 (0.88)⁹

= 8495 (0.3164)

F₉ = 2688.48

Problem 3 :

a. If buy a car for $38500 and keep it for 3 years, what will its value be at the end of that period given that its annual depreciation rate is 20% ?

b. By how much did it depreciate?

Solution:

a.

Given, P_v = 38500

i = 20% = 0.2

n = 3

F_v = P_v (1 - i)ⁿ

F_v = 38500 (1 - 0.2)³

= 38500 (0.8)³

= 38500 (0.512)

= $19712

b. 

Depreciate = $38500 - $19712

= $18788

Problem 4 :

A cabin cruiser was bought for $120000 in April 1998 and was sold for $45000 in April 2006. At what average annual rate of depreciation did the boat lose its value?

Solution:

Given, P_v = $120000

F_v = $45000

n = 8

F_v = P_v (1 - i)ⁿ

Problem 5 :

A small jet aeroplane was purchased for 3.4 million dollars in January 1998 and was sold for 2.35 million dollars in July 2005. What was its average annual rate of depreciation over this peroid?

Solution:

Given, P_v = 3.4 million dollars

F_v = 2.35 million dollars

n = 7

F_v = P_v (1 - i)ⁿ

2.35 = 3.4(1 - i)ⁿ

2.35/3.4 = (1 - i)⁷

0.69 =  (1 - i)⁷

log 0.69 = log(1 - i)⁷

log 0.69 = 7 log(1 - i)

log 0.69/7 = log (1 - i)

-0.0230 = log(1 - i)

0.9523 = 1 - i

i = 1 - 0.9487

i = 0.0477

Rate of depreciation = 0.0477 x 100%

= 4.77 %

Approximately 4.8%.