WORD PROBLEMS INVOLVING AREA OF SIMILAR SHAPES

If the sides of a rectangle are multiplied by k, a similar rectangle is obtained.

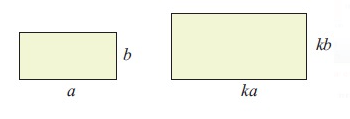
The new area = ka × kb

= k² ab

= k² × the old area

If an object or figure is enlarged by a scale factor of k, then

 the area of the image = k² × the area of the object

Problem 1 :

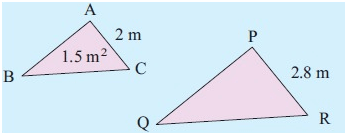
Triangles ABC and PQR are similar and the area of triangle ABC is 1.5 m². What is the area of triangle PQR?

Solution :

Corresponding side of AC is PR.

Ratio between small shape to large shape :

AC : PR = 2 : 2.8

AC/PR = 2/2.8

AC/PR = 1/1.4

Scale factor (k) = 1.4

Area of PQR = k² × area of ABC

x = k² × 1.5

x = (1.4)² × 1.5

= 1.96 × 1.5

= 2.94

So, the area of triangle PQR is 2.94 m².

Problem 2 :

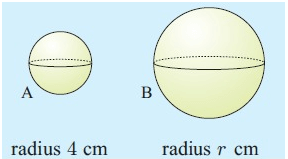
Two spheres have surface areas of 201 cm² and 452 cm² respectively. Find the radius of the larger sphere.

Solution :

Area of larger sphere = k² × area of small sphere

452 = k² × 201

k² = 452/201

k² = 2.25

k = 1.5

Radius of larger sphere = k × radius of small sphere

r = 1.5 × 4

r = 6

So, radius of larger sphere is 6 cm.

Problem 3 :

The sides of a triangular stained glass window pane are 5 m, 6 m and 7 m. Another pane is similar to it with longest side 21 m. Find :

a) The scale factor b the lengths of the other two sides

c) The ratio of the areas of the two panes.

Solution :

a) Scale factor :

Longest side of smaller pane is 7 m, corresponding side of larger pane is 21 cm.

Longest side of the larger pane = k × Longest side of the smaller pane

21 = k × 7

k = 21/7

k = 3

b) The lengths of the other two sides of the larger pane be a and b these are corresponding side of 5 m and 6 m.

a = 5 × 3 = 15 m

b = 6 × 3 = 18 m

So, the lengths of the other two sides is 15 m and 18 m.

c) The ratio of the areas of the two panes.

Area of larger pane = k² × Area of smaller pane

Area of larger pane/ Area of smaller pane = 9/1

Area of larger pane : Area of smaller pane = 9:1

Problem 4 :

Two rectangular photographs are similar and one has area double the other.

a) What is the scale factor?

b) If the larger one is 20 cm by 10 cm, what are the dimensions of the smaller one?

Solution :

a) Area of larger rectangle = k² x area of smaller rectangle

Area of larger rectangle/area of smaller rectangle

= k²/1 -------(1)

Area of larger rectangle = 2 area of smaller rectangle

Area of larger rectangle/area of smaller rectangle

= 2/1  -------(2)

(1) = (2)

k²/1 = 2/1

k² = 2

k = √2

b) Length of the larger rectangle = k × length of smaller rectangle

20 = √2 × length of smaller rectangle

length of smaller rectangle = 20/√2

= 14.14 cm

Width of the larger rectangle = k × width of smaller rectangle

10 = √2 × width of smaller rectangle

width smaller rectangle = 10/√2

= 7.07 cm

So, the dimensions of the smaller rectangle is 14.14 cm by 7.07 cm.

Problem 5 :

Two circles are such that one has area three times the other.

a) What is the scale factor?

b) If the smaller circle has a circumference of 35.8 m, what is the circumference of the larger one?

Solution :

a) Area of larger circle = k² x area of smaller circle

Area of larger circle/area of smaller circle

= k²/1 -------(1)

Area of larger circle = 2 area of smaller circle

Area of larger circle/area of smaller circle

= 3/1  -------(2)

(1) = (2)

k²/1 = 3/1

k² = 3

k = √3

b) Circumference of large circle = k × Circumference of small circle

Circumference of large circle = √3 × 35.8

Circumference of small circle = 35.8√3

= 62.0 m