WITH THE GIVEN INPUTS AND OUTPUTS ARE THERE ANY GUARANTEED EXTREMA

Let 𝒇(𝒙) be a polynomial function with the given values. Are there any guaranteed extrema? If so, state where they occur.

Problem 1 :

f(-1) = 0, f(0) = 6 and f(6) = 0

Solution :

By observing the inputs and outputs,

f(0) > f(-1)

f(6) < f(0)

• In the interval [-1, 0] the function must be increasing because considering the outputs 6 is greater than the previous output 0.
• In the interval [0, 6] the function must be decreasing because considering the outputs 0 is lesser than the previous output 6.

The curve changes its path from increasing to decreasing, then there must be guaranteed extrema in the interval [-1, 6].

Problem 2 :

f(0) = 6, f(3) = 2, f(6) = 0 and f(10) = 0

Solution :

By observing the inputs and outputs,

f(3) < f(0)

f(6) < f(3)

f(6) and (10) = 0

• In the interval [0, 3] the function must be decreasing because considering the outputs 2 is lesser than the previous output 6.
• In the interval [3, 6] the function must be decreasing because considering the outputs 0 is lesser than the previous output 2.

The curve doesn't changes its direction in the interval [0, 3], by ploting the points in the grid, we get

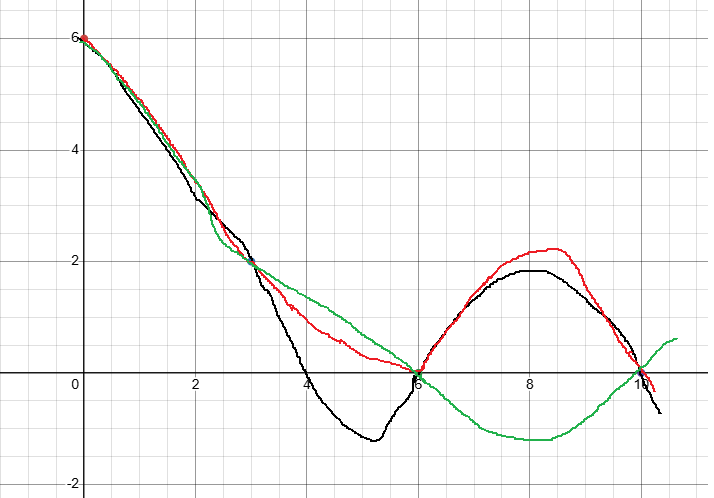
As we can draw many possible curves. We observe there must be maximum or minimum. so, extrema is guaranteed.

Problem 3 :

f(-5) = 0, f(0) = 5 and f(5) = 7

Solution :

By observing the inputs and outputs,

f(0) > f(- 5)

f(5) > f(0)

Continuousely it is increasing, there is no change in the path. So, there is no guarantee.

Problem 4 :

f(0) = -2, f(1) = 0 and f(11) = 0

Solution :

By observing the inputs and outputs,

f(1) > f(0)

f(1) = f(11)

•  In the interval [0, 1], it is increasing since 0 is greater than -2.
• The x-intercepts are 1 and 11. In between these two values, we may draw many possible curves.

As we can draw many possible curves. We observe there must be maximum or minimum. so, extrema is guaranteed.

Find the following extrema. If there are none, cross it off and write NONE.

Problem 5 :

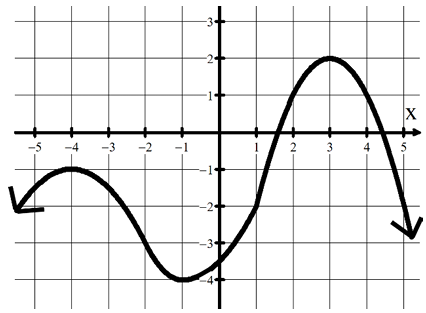
a)  Absolute min of _____ when 𝑥 = 

b) Absolute max of _____ when 𝑥 = 

c)  Relative min(s) at 𝑥 = 

d)  Relative max(es) at 𝑥 = 

Solution :

a)  Absolute min of -4 when 𝑥 = -1

b) Absolute max of 2 when 𝑥 = 3

c)  Relative min(s) at 𝑥 = -1

d)  Relative max(es) at 𝑥 = -4 and 3

Problem 6 :

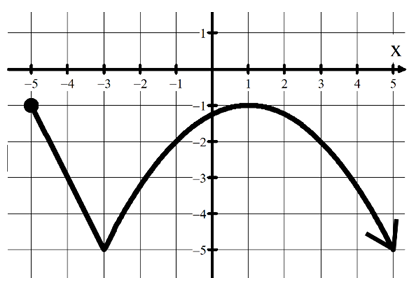
a) Absolute min of _____ when 𝑥 =

b) Absolute max of _____ when 𝑥 =

c)  Relative min(s) at 𝑥 = 

d)  Relative max(es) at 𝑥 =

Solution :

a) Absolute min of -5 when 𝑥 = -3

b) Absolute max of -1 when 𝑥 = 1 and -5

c)  Relative min(s) at 𝑥 = -3

d)  Relative max(es) at 𝑥 = -5 and 1

Problem 7 :

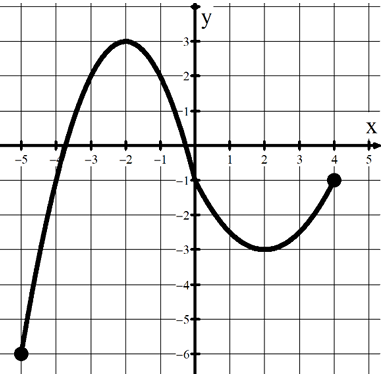
a)  Absolute min of _____ when 𝑥 = 

b)  Absolute max of _____ when 𝑥 = 

c)  Relative min(s) at 𝑥 =

d)  Relative max(es) at 𝑥 = 

Solution :

a)  Absolute min of -6 when 𝑥 = 5

b)  Absolute max of 3 when 𝑥 = -2

c)  Relative min(s) at 𝑥 = 2 and -5

d)  Relative max(es) at 𝑥 = -2 and 4.

Problem 8 :

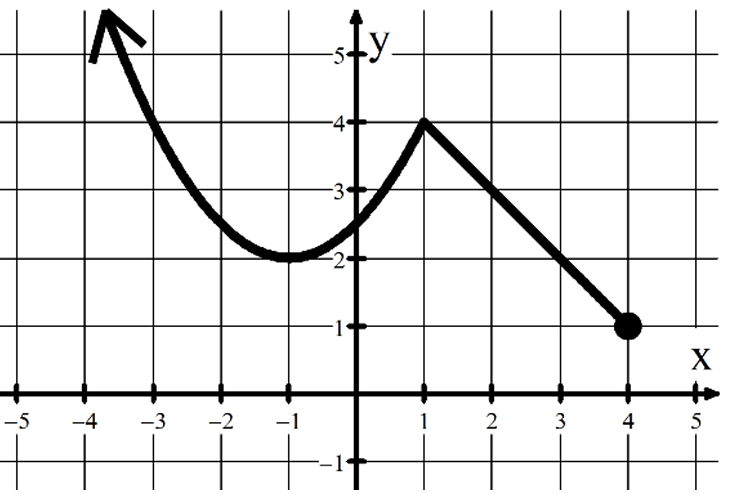
a)  Absolute min of _____ when 𝑥 = 

b)  Absolute max of _____ when 𝑥 =

c)  Relative min(s) at 𝑥 =

d)  Relative max(es) at 𝑥 = 

Solution :

a)  Absolute min of 2 when 𝑥 = -1

b)  Absolute max of _____ when 𝑥 =

There is no absolute maximum, since we have a sharp edge at maximum.

c)  Relative min(s) at 𝑥 = -1 and 4

d)  Relative max(es) at 𝑥 = 1

Problem 9 :

The values of a function are given at selected 𝑥-values in the table below. The function’s concavity does not change. Determine if the function is concave up or concave down. Justify your answer.

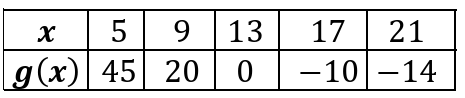
Solution :

• When rate of changes increases, the function must be increasing function and concave up in the interval.
• When rate of changes decreases, the function must be decreasing function and concave down in the interval.
• Note x-values are sapaced equally.

Average rate of change of (5, 45) and (9, 20) :

 = (20 - 45) / (9 - 5)

= -25/4

Average rate of change of (9, 20) and (13, 0) :

 = (0 - 20) / (13 - 9)

= -20/4

 = -5

Average rate of change of (13, 0) and (17, -10)

 = (-10 - 0) / (17 - 13)

= -10/4

 = -2.5

Average rate of change of (17, -10) and (21, -14)

 = (--14 + 10) / (21 - 17)

= -4/4

 = -1

Since the rate of change is increasing the curve must be concave up in the interval.