WHEN TWO ZEROES OF CUBIC POLYNOMIAL IS GIVEN FIND TEH OTHER ZERO

Problem 1 :

Find all the zeroes of the polynomial x³ + 3x² – 2x – 6, if two of its zeroes are -√2 and √2.

Solution :

Given, polynomial x³ + 3x² – 2x – 6

Two of its zeroes are  -√2 and √2

(x – (-√2)) and (x – (√2))

(x + √2) (x - √2)

x² - x√2 + x√2 – 2

x² – 2

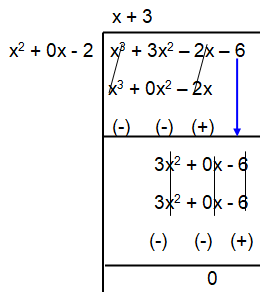
x + 3 = 0

x = -3

All the zeroes are -√2, √2 and -3

Problem 2 :

Find all the zeroes of the polynomial 2x³ + x² – 6x – 3, if two of its zeroes are -√3 and √3.

Solution :

Given, polynomial 2x³ + x² – 6x – 3

Two of its zeroes are -√3 and √3

(x – (-√3)) and (x – (√3))

(x + √3) (x - √3)  

x² - x√3 + x√3 – 3

x² – 3

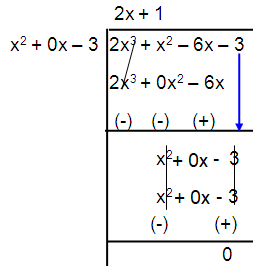
2x + 1 = 0

2x = -1

x = -1/2

All the zeroes are -√3, √3 and -1/2.

Problem 3 :

Obtain all other zeroes of the polynomial 2x³ - 4x – x² + 2, if two of its zeroes are √2 and -√2.

Solution :

Given, polynomial 2x³ – x² – 4x + 2

Two of its zeroes are -√2 and -√2

(x – (√2)) and (x – (-√2))

(x - √2) (x + √2)  

x² + x√2 - x√2 – 2

x² – 2

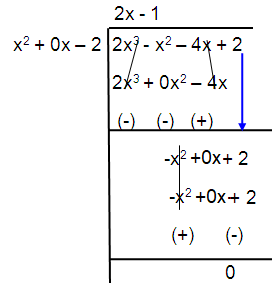
2x - 1 = 0

2x = 1

x = 1/2

All the zeroes are - √2, -√2 and 1/2.

Problem 4 :

If the polynomial 6x⁴ + 8x³ + 17x² + 21x + 7 is divided by another  polynomial 3x² + 4x + 1 then the remainder comes out to be ax + b, find ‘a’ and ‘b’. 

Solution :

Given, polynomial 6x⁴ + 8x³ + 17x² + 21x + 7

Divided by another polynomial 3x² + 4x + 1

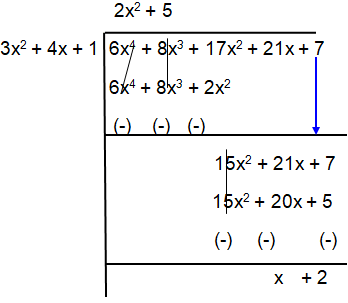
Remainder comes out to be ax + b,

x + 2

To find ‘a’ and ‘b’ :

a = 1, b = 2

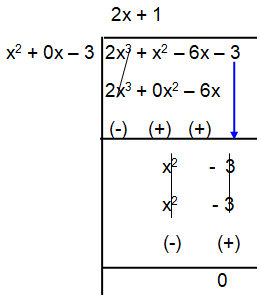
2x + 1 = 0

2x = -1

x = -1/2

All the zeroes are -√3, √3 and -1/2.